【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

参考答案:
【答案】(1)点A坐标为(1,4),y=﹣x2+2x+3;(2)当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
【解析】试题分析:(1)根据矩形的三个顶点坐标以及抛物线的对称轴可求出点A的坐标;设抛物线的解析式为顶点式,然后把点A、C坐标代入计算即可;(2)分∠QPC=90°和∠PQC=90°两种情况讨论,利用比例线段可求出t的值;(3)求出直线AC的解析式,然后把点P(1,4﹣t)的纵坐标代入,然后用t可表示出点Q的坐标,以及QF的长,然后可求出△ACQ的面积与t的函数关系式,利用二次函数的性质确定函数值的值即可.
试题解析:解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依题意有:OC=3,OE=4,
∴CE=![]() =
=![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QPC=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ;
;
当∠PQC=90°时,
∵cos∠QCP=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
∴当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q点的横坐标为1+![]() ,
,
将x=1+![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣![]() .
.
∴Q点的纵坐标为4﹣![]() ,
,
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ=S△AFQ+S△CPQ
=![]() FQAG+
FQAG+![]() FQDG
FQDG
=![]() FQ(AG+DG)
FQ(AG+DG)
=![]() FQAD
FQAD
=![]() ×2(t﹣
×2(t﹣![]() )
)
=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面不是同类项的是( )
A. ﹣2与5 B. ﹣2a2b与a2b C. ﹣x2y2与6x2y2 D. 2m与2n
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,不适宜采用全面调查(普查)的是( )
A. 旅客上飞机前的安检 B. 学校招聘教师,对应聘人员面试
C. 了解全班同学期末考试的成绩情况 D. 了解一批灯泡的使用寿命
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距200km的A,B两地同时出发,它们离A地的距离s(km)随时间t(h)变化的图象如图所示,则下列结论不正确的是( )

A. 甲车的平均速度为40km/h
B. 乙车行驶3h到达A地,稍作停留后返回B地
C. 经
 h后,两车在途中相遇
h后,两车在途中相遇D. 乙车返回B地的平均速度比去A地的平均速度小
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
A、y=0.05xB、y=5x
C、y=100xD、y=0.05x+100
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截下列几何体,截面可能是圆的是________(填写序号).
①三棱柱 ②圆锥 ③圆柱 ④长方体 ⑤球体
-
科目: 来源: 题型:
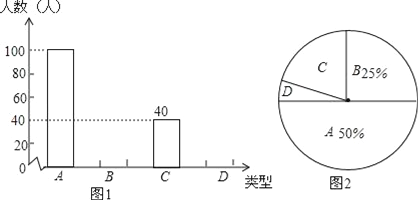
查看答案和解析>>【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
相关试题

