【题目】如图1,抛物线y=-![]() x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.

(1)求该抛物线的函数表达式;
(2)求点C的坐标和线段EF的长;
(3)如图2,连接CD并延长,交直线l于点N,点P,Q为射线NB上的两个动点(点P在点Q的右侧,且不与N重合),线段PQ与EF的长度相等,连接DP,CQ,四边形CDPQ的周长是否有最小值?若有,请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值;若没有,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=-![]() x2-
x2-![]() x+4.(2)2.(3)2
x+4.(2)2.(3)2![]() +2
+2![]() +2.
+2.
【解析】
试题分析:(1)根据点A的坐标和tan∠BAO=2求得AO=2,BO=4,从而求得点B的坐标为(0,4),利用待定系数法求得二次函数的解析式即可.
(2)首先根据抛物线的对称轴求得点A的对称点C的坐标,然后求得点B的对称点E的坐标为(-1,4),从而求得BE的长,得到EF的长即可;
(3)作点D关于直线l的对称点D1(1,6),点C向右平移2个单位得到C1(-1,0),连接C1D1与直线l交于点P,点P向左平移两个单位得到点Q,四边形CDPQ即为周长最小的四边形.
试题解析:(1)∵点A(2,0),tan∠BAO=2,
∴AO=2,BO=4,
∴点B的坐标为(0,4).
∵抛物线y=-![]() x2+bx+c过点A,B,
x2+bx+c过点A,B,
∴ ,
,
解得 ,
,
∴此抛物线的解析式为y=-![]() x2-
x2-![]() x+4.
x+4.
(2)∵抛物线对称轴为直线x=-![]() ,
,
∴点A关于对称轴的对称点C的坐标为(-3,0),
点B的对称点E的坐标为(-1,4),
∵BC是⊙M的直径,
∴点M的坐标为(-![]() ,2),
,2),
如图1,过点M作MG⊥FB,则GB=GF,

∵M(-![]() ,2),
,2),
∴BG=![]() ,
,
∴BF=2BG=3,
∵点E的坐标为(-1,4),
∴BE=1,
∴EF=BF-BE=3-1=2.
(3)四边形CDPQ的周长有最小值.
理由如下:∵BC=![]() =
=![]() =5,
=5,
AC=CO+OA=3+2=5,
∴AC=BC,
∵BC为⊙M直径,
∴∠BDC=90°,即CD⊥AB,
∴D为AB中点,
∴点D的坐标为(1,2).
如图2,作点D关于直线l的对称点D1(1,6),点C向右平移2个单位得到C1(-1,0),连接C1D1与直线l交于点P,点P向左平移2个单位得到点Q,四边形CDPQ即为周长最小的四边形.

设直线C1D1的函数表达式为y=mx+n(m≠0),
∴![]() ,
,![]() ,
,
∴直线C1D1的表达式为y=3x+3,
∵yp=4,
∴xp=![]() ,
,
∴点P的坐标为(![]() ,4);
,4);
C四边形CDPQ最小=2![]() +2
+2![]() +2.
+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD相交于点O,∠ABC∶∠BAD=1∶2,AC∥BE,CE∥BD.
(1)求∠DBC的度数;
(2)求证:四边形OBEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
 在平面直角坐标系中按图中箭头所示方向运动,第
在平面直角坐标系中按图中箭头所示方向运动,第 次从原点运动到点
次从原点运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,
, 按这样的运动规律,经过第
按这样的运动规律,经过第 次运动后,动点
次运动后,动点 的坐标是( )
的坐标是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
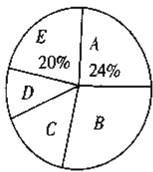
查看答案和解析>>【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
级别
家庭的文化教育消费金额
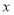 (元)
(元)户数
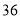

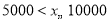
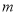
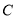
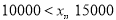
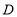
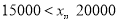
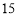
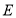
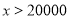
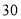
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有___________户,表中
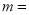 ___________;
___________;(2)在扇形统计图中,
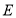 组所在扇形的圆心角为多少度?
组所在扇形的圆心角为多少度?(3)这个社区有
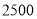 户家庭,请你估计年文化教育消费在
户家庭,请你估计年文化教育消费在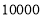 元以上的家庭有多少户.
元以上的家庭有多少户. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是________、________.
(2)将△ABC平移后使点C与点D重合,点A、B分别与点E、F重合,画出△DEF.并直接写出E点的坐标 ,F点的坐标 .
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为___ _____.
(4)求
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
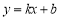 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6,
的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6, ),DE=3.
),DE=3.(1)求反比例函数与一次函数的解析式.
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂从2011年起开始投入技改资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表所示:
年度
2011
2012
2013
2014
投入技改资金
 /万元
/万元2.5
3
4
4.5
产品成本
 /(万元/件)
/(万元/件)7.2
6
4.5
4
(1)请认真分析表中的数据,从你学过的一次函数和反比例函数中确定哪种函数能表示其变化规律,并求出它的表达式;
(2)按照这种变化规律,2015年已投入技改资金5万元.
①预计产品成本每件比2014年降低多少万元?
②如果打算在2015年把每件产品的成本降低到3.2万元,那么还需投入技改资金多少万元?(精确到0.01万元)
相关试题

