【题目】我们定义:如图1,在△ABC中,把AB绕点A按顺时针方向旋转α(0°<α<180°)得到AB′,把AC绕点A按逆时针方向旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的“旋补三角形”,△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
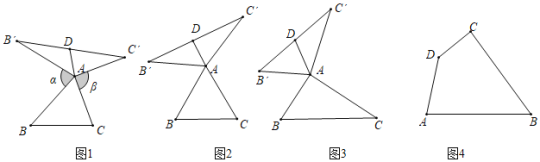
(1)特例感知:在图2、图3中,△AB′C′是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=______BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为______.
(2)精确作图:如图4,已知在四边形ABCD内部存在点P,使得△PDC是△PAB的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点P(要求:保留作图痕迹,不写作法和证明)
(3)猜想论证:在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
参考答案:
【答案】(1)①![]() ,②4;(2)见解析;(3)AD=
,②4;(2)见解析;(3)AD=![]() BC.
BC.
【解析】
(1)①根据含30°直角三角形的性质解答;②证明△AB′C′≌△ABC,根据全等三角形的性质得到B′C′=BC,根据直角三角形的性质计算;
(2)根据线段垂直平分线的性质、利用尺规作图作出点P;
(3)证明四边形AB′EC′是平行四边形,得到B′E=AC′,∠B′AC′+∠AB′E=180°,根据全等三角形的性质得到AE=BC,得到答案.
解:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=120°,AB=AB′,AC=AC′,
∴AB′=AC′,
∴∠AB′D=30°,
∴AD=![]() AB′,
AB′,
∴AD=![]() BC,
BC,
故答案为:![]() ;
;
②∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=∠BAC=90°,AB=AB′,AC=AC′,
在△AB′C′和△ABC中,
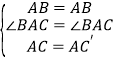 ,
,
∴△AB′C′≌△ABC(SAS)
∴B′C′=BC=8,
∵∠B′AC′=90°,AD是△ABC的“旋补中线”,
∴AD=![]() B′C′=4,
B′C′=4,
故答案为:4;
(2)如图4,作线段AD、BC的垂直平分线,交点即为点P,

∴点P即为所作;
(3)AD=![]() BC,
BC,
证明:如图1,延长AD到E,使得DE=AD,连接B′E、C′E,
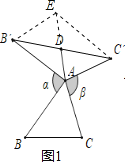
∵AD是△AB′C’的中线,
∴B′D=C′D,
∵DE=AD,
∴四边形AB′EC′是平行四边形,
∴B′E=AC′,∠B′AC′+∠AB′E=180°,
∵α+β=180°,
∴∠B′AC′+∠BAC=180°,
∴∠EB′A=∠BAC,
在△EB′A和△CAB中,
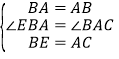
∴△EB′A≌△CAB(SAS),
∴AE=BC,
∴AD=![]() BC.
BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,对“学习习惯”进行问卷调查.
设计的问题:对自己做错的题目进行整理、分析、改正;
答案选项为:A:很少,B:有时,C:常常,D:总是;
将调查结果的数据进行了整理、绘制成部分统计图如下:
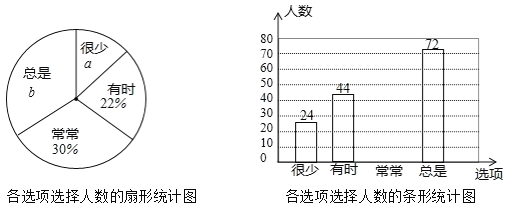
请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,a= %,b= %,“常常”对应扇形的圆心角为 ;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名?
-
科目: 来源: 题型:
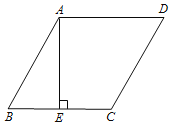
查看答案和解析>>【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.
-
科目: 来源: 题型:
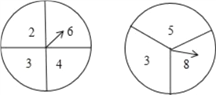
查看答案和解析>>【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.
小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)
-
科目: 来源: 题型:
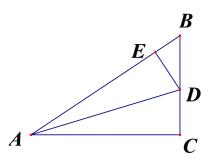
查看答案和解析>>【题目】已知:如图,Rt△ABC中,∠C=90°,AC=8,BC=6,AD平分∠BAC,交BC于点D,DE⊥AB于点E.
(1)求BE的长;
(2)求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年9月,在郑州举行的第十一届全国少数民族运动会的龙舟比赛中,甲、乙两队在
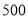 米的赛道上,所划行的路程
米的赛道上,所划行的路程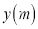 与时间
与时间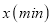 之间的函数关系式如图所示,下列说法错误的是( )
之间的函数关系式如图所示,下列说法错误的是( )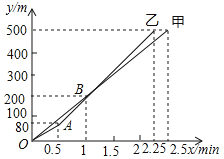
A.乙队比甲队提前
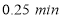 到达终点
到达终点B.当乙队划行
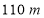 时,此时落后甲队
时,此时落后甲队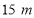
C.
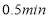 后,乙队比甲队每分钟快
后,乙队比甲队每分钟快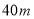
D.自
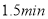 开始,甲队若要与乙队同时到达终点,甲队的速度需提高到
开始,甲队若要与乙队同时到达终点,甲队的速度需提高到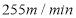
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
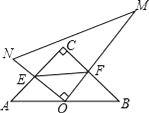
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
相关试题

