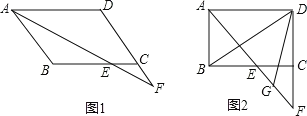
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
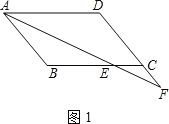
(1)在图1中说明CE=CF;
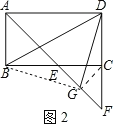
(2)若∠ABC=90°,G是EF的中点(如图2),求∠BDG的度数.
参考答案:
【答案】(1)答案见解析;(2)∠BDG=45°.
【解析】
(1)先根据角平分线的定义可得![]() ,再根据平行四边形的性质、平行线的性质可得
,再根据平行四边形的性质、平行线的性质可得![]() ,从而可得
,从而可得![]() ,然后根据等腰三角形的性质即可得证;
,然后根据等腰三角形的性质即可得证;
(2)先根据矩形的性质和题(1)的结论可得出![]() 为等腰直角三角形,再根据等腰三角形的性质可得
为等腰直角三角形,再根据等腰三角形的性质可得![]() ,然后根据角平分线的定义、等腰三角形的判定与性质可得
,然后根据角平分线的定义、等腰三角形的判定与性质可得![]() ,从而可得
,从而可得![]() ,最后根据三角形全等的判定定理与性质可得
,最后根据三角形全等的判定定理与性质可得![]() ,从而可推出
,从而可推出![]() 为等腰直角三角形,由此即可得出答案.
为等腰直角三角形,由此即可得出答案.
(1)如图1,AF平分![]()
![]()
∵四边形ABCD是平行四边形
![]()
![]()
![]()
![]() ;
;
(2)如图2,连接GC、BG
∵四边形ABCD为平行四边形,![]()
∴四边形ABCD为矩形
![]()
![]()
结合(1)的结论得,![]() 为等腰直角三角形
为等腰直角三角形
∵G为EF中点
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
又![]() AF平分
AF平分![]() ,
,![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
![]()
![]()
![]() ,即
,即![]()
在![]() 与
与![]() 中,
中,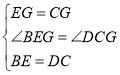
![]()
![]()
![]()
![]()
![]()
![]() 为等腰直角三角形
为等腰直角三角形
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有( )
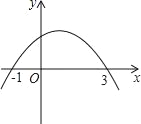
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
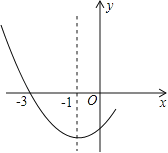
A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

