【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量容量是______________,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

参考答案:
【答案】(1)、50;图形见解析;(2)、90;(3)、![]() .
.
【解析】
试题分析:(1)、根据题意得出B的百分比,然后得出人数,根据C的百分比得出C组别的人数,然后进行补全;(2)、首先求出不少于12的频率,然后进行计算;(3)、根据题意画出树状图,然后得出概率.
试题解析:(1)、根据题意得:B:8%=5:2 则B=20% 10÷20%=50
C组别的人数:50×30%=15(人)
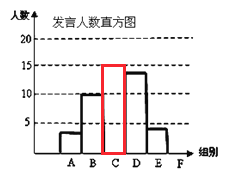
(2)、∵在统计的50人中,发言次数大于12的有4+5=9人,∴在这天里发言次数不少于12的频率为9÷50=18%。∴全年级500人中,在这天里发言次数不少于12的次数为500×18%=90(次)。
(3)、∵A组发言的学生为3人,∴有1位女生,2位男生。∵E组发言的学生: 4人,
∴有2位女生,2位男生。∴由题意可画树状图为:

∴共有12种情况,所抽的两位学生恰好是一男一女的情况有6种,∴所抽的两位学生恰好是一男一女的概率为![]() =
=![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?答: (填“成立”或“不成立”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.(ab2)3=ab6
B.(3xy)3=9x3y3
C.(﹣2a2)2=4a4
D.(ab)3=ab3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.
(1)求证:AF﹣BF=EF;
(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】0.00813用科学记数法表示为( )
A.8.13×10﹣3
B.81.3×10﹣4
C.8.13×10﹣4
D.81.3×10﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=
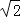 ,求AD和AB的长.
,求AD和AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式2x2﹣8因式分解的结果是______.
相关试题

