【题目】在ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为( )
A. 8或24B. 8C. 24D. 9或24
参考答案:
【答案】A
【解析】
因为BE平分∠ABC,所以∠ABE=∠CBE,因为四边形ABCD是平行四边形,所以AD∥BC,可证得AB=AE=6,点E将AD分为1:3两部分,可得DE=18或DE=2两种情况,分别讨论即可求解.
解:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BEA=∠CBE,
∴∠ABE=∠BEA,
∴AB=AE=6.
∵点E将AD分为1:3两部分,
∴DE=18或DE=2,
∴当DE=18时,AD=24;
当DE=2,AD=8;
故选:A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、AD、BD. 已知圆O的半径长为5 ,弦AB的长为8.
(1)如图1,当点D是弧AB的中点时,求CD的长;
(2)如图2,设AC=x,
 ,求y关于x的函数解析式并写出定义域;
,求y关于x的函数解析式并写出定义域;(3)若四边形AOBD是梯形,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=
 AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )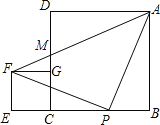
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与x轴,y轴分别交于A,B两点,点
与x轴,y轴分别交于A,B两点,点 为直线
为直线 上一点,直线
上一点,直线 过点C.
过点C.
 求m和b的值;
求m和b的值; 直线
直线 与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动
与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动 设点P的运动时间为t秒.
设点P的运动时间为t秒.①若点P在线段DA上,且
 的面积为10,求t的值;
的面积为10,求t的值;②是否存在t的值,使
 为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
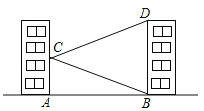
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在
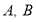 两地分别库存挖掘机
两地分别库存挖掘机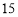 台和
台和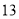 台,现在运往甲、乙两地文扳建设,其中甲地需要
台,现在运往甲、乙两地文扳建设,其中甲地需要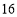 台,乙地需要
台,乙地需要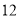 台,从
台,从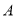 地运
地运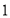 台挖掘机到甲、乙两地的费用分别是
台挖掘机到甲、乙两地的费用分别是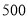 元和
元和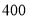 元:从
元:从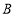 地运
地运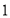 台挖掘机到甲、乙两地的费用分别是
台挖掘机到甲、乙两地的费用分别是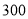 元和
元和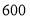 元
元(1)设从
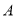 地运往甲地
地运往甲地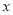 台挖掘机,请补全下表.
台挖掘机,请补全下表.甲
乙
总计
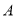
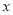 台
台台
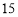 台
台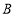
台
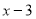 台
台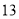 台
台总计
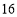 台
台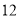 台
台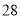 台
台(2)当从
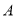 地运往甲地
地运往甲地 台挖掘机时,运这批挖掘机的总费用是多少?
台挖掘机时,运这批挖掘机的总费用是多少?
相关试题

