搜索
【题目】某公司在
两地分别库存挖掘机
台和
台，现在运往甲、乙两地文扳建设，其中甲地需要
台，乙地需要
台，从
地运
台挖掘机到甲、乙两地的费用分别是
元和
元:从
地运台挖掘机到甲、乙两地的费用分别是
元和
元
（1）设从地运往甲地
台挖掘机，请补全下表.
甲 | 乙 | 总计 | |
|
| 台 |
|
| 台 |
|
|
总计 |
|
|
|
（2）当从地运往甲地
台挖掘机时，运这批挖掘机的总费用是多少?
参考答案：
【答案】（1）见解析；（2）
元
【解析】
（1）根据表格即可写出从
地运往乙地为（
）台，从B地运往甲地为（
）台；
（2）当x＝4时，根据表格求出A,B运算的台数，再进行求解.
（1）从地运往乙地为（）台，从B地运往甲地为（）台；
补全表格如下：
甲 | 乙 | 总计 | |
|
|
|
|
|
|
|
|
总计 |
|
|
|
（2）当从地运往甲地
台挖掘机时，即x=4,
∴从地运往乙地11台挖掘机；
从B地运往甲地12台挖掘机；
从B地运往乙地1台挖掘机；
故总费用为：500×4+400×11+300×12+600×1=（元）
答：当从A地运往甲地4台挖掘机时，运这批挖掘机的总费用是10600元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在ABCD中，已知AB＝6，BE平分∠ABC交AD边于点E，点E将AD分为1：3两部分，则AD的长为（ ）
A. 8或24B. 8C. 24D. 9或24
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
与x轴，y轴分别交于A，B两点，点
为直线上一点，直线
过点C．
求m和b的值；
直线与x轴交于点D，动点P从点D开始以每秒1个单位的速度向x轴负方向运动
设点P的运动时间为t秒．①若点P在线段DA上，且
的面积为10，求t的值；②是否存在t的值，使
为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由． -
科目： 来源： 题型：
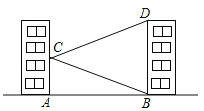
查看答案和解析>>【题目】如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m．
（1）求∠BCD的度数．
（2）求教学楼的高BD．（结果精确到0.1m，参考数据：tan20°≈0.36，tan18°≈0.32）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的对角线AC，BD相交于点O，点E是AC的一点，连接EB，过点A做AM⊥BE，垂足为M，AM与BD相交于点F．
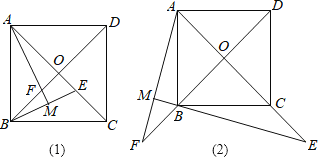
（1）猜想：如图（1）线段OE与线段OF的数量关系为 ；
（2）拓展：如图（2），若点E在AC的延长线上，AM⊥BE于点M，AM、DB的延长线相交于点F，其他条件不变，（1）的结论还成立吗？如果成立，请仅就图（2）给出证明；如果不成立，请说明理由．
-
科目： 来源： 题型：
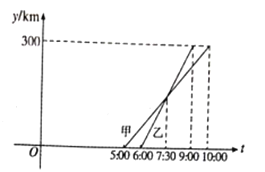
查看答案和解析>>【题目】甲、乙两车从
城出发前往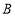
城，在整个行程中，汽车离开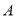城的距离
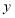与时刻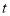
的对应关系如右图所示.（1）
、两城相距多远？（2）哪辆车先出发？哪辆车先到
城？（3）甲、乙两车的平均速度分别为多少？
（4）你还能从图中得到哪些信息？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题10分）某自行车厂一周计划生产700辆自行车，平均每天生产自行车100辆，由于各种原因，实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况（超计划生产量为正、不足计划生产量为负，单位：辆）：
星期
一
二
三
四
五
六
日
增减
＋8
－2
－3
+16
－9
+10
－11
（1）根据记录可知前三天共生产自行车 辆；
（2）产量最多的一天比产量最少的一天生产 辆；
（3）若该厂实行按生产的自行车数量的多少计工资，即计件工资制。如果每生产一辆自行车就可以得人民币60 元，超额完多成任务，每超一辆可多得 15 元；若不足计划数的，每少生产一辆扣 15 元，那么该厂工人这一周的工资总额是多少？
相关试题
