【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: 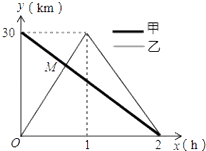
(1)写出A、B两地之间的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
参考答案:
【答案】
(1)解:x=0时,甲距离B地30千米,
所以,A、B两地的距离为30千米
(2)解:由图可知,甲的速度:30÷2=15千米/时,
乙的速度:30÷1=30千米/时,
30÷(15+30)= ![]() ,
, ![]() ×30=20千米,
×30=20千米,
所以,点M的坐标为( ![]() ,20),表示甲、乙两人出发
,20),表示甲、乙两人出发 ![]() 小时后相遇,此时距离B地20千米;
小时后相遇,此时距离B地20千米;
(3)解:设x小时甲、乙两人相距3km,
①若是相遇前,则15x+30x=30﹣3,解得x= ![]() ,
,
②若是相遇后,则15x+30x=30+3,解得x= ![]() ,
,
③若是甲到达B地前,而乙到达A地后按原路返回时,
则15x﹣30(x﹣1)=3,
解得x= ![]() ,
,
所以,当 ![]() ≤x≤
≤x≤ ![]() 或
或 ![]() ≤x≤2时,甲、乙两人能够用无线对讲机保持联系
≤x≤2时,甲、乙两人能够用无线对讲机保持联系
【解析】(1)根据x=0时,甲距离B地30千米,由此即可解决问题.(2)根据相遇时间= ![]() 即可解决.(3)分三个时间段求出时间即可,①是相遇前,则15x+30x=30﹣3,②是相遇后,则15x+30x=30+3,③若是甲到达B地前,而乙到达A地后按原路返回时,则15x﹣30(x﹣1)=3,分别解方程即可.
即可解决.(3)分三个时间段求出时间即可,①是相遇前,则15x+30x=30﹣3,②是相遇后,则15x+30x=30+3,③若是甲到达B地前,而乙到达A地后按原路返回时,则15x﹣30(x﹣1)=3,分别解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工人师傅砌门时,常用一根木条固定长方形门框,使其不变形,这样做的根据( )
A. 两点之间的线段最短 B. 三角形具有稳定性
C. 长方形是轴对称图形 D. 长方形的四个角都是直角
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2C垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2,y=﹣3是二元一次方程5x+my+2=0的解,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)0等于( )
A.1
B.﹣1
C.﹣3
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.
(1)请求出两种口味的粽子每盒的价格;
(2)设买大枣粽子x盒,买水果共用了w元. ①请求出w关于x的函数关系式;
②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多. -
科目: 来源: 题型:
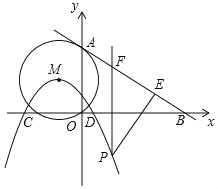
查看答案和解析>>【题目】如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A,经过点A的一条直线l解析式为:y=﹣
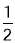 x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).(1)求抛物线的解析式;
(2)求证:直线l是⊙M的切线;
(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E,PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小?若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.
相关试题

