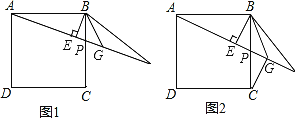
【题目】已知如图1,P为正方形ABCD的边BC上任意一点,BE⊥AP于点E,在AP的延长线上取点F,使EF=AE,连接BF,∠CBF的平分线交AF于点G.
(1)求证:BF=BC;
(2)求证:△BEG是等腰直角三角形;
(3)如图2,若正方形ABCD的边长为4,连接CG,当P点为BC的中点时,求CG的长.
参考答案:
【答案】(1)证明见解析;92)证明见解析;(3)![]()
【解析】(1)利用线段的垂直平分线的性质以及正方形的性质即可证明;
(2)想办法证明∠F=∠BAF=∠EBP,由∠EBG=∠EBP+∠PBG,∠EGB=∠F+∠GBF,即可解决问题;
(3)求出BG,只要证明△EBP≌△GCP,即可推出CG=BE,由此即可解决问题.
解:(1)证明:∵BE⊥AP,AE=EF,
∴BE垂直平分线段AF,
∴AB=BF,
在正方形ABCD中,AB=BC,
∴BF=BC;
(2)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠EBP=90°,
∵BE⊥AF,
∴∠ABE+∠BAP=90°,
∴∠BAP=∠EBP,
∵AB=BF∴∠BAP=∠BFP,
∴∠EBP=∠BFP,
∵∠CBF的平分线交AF于点G,
∴∠CBG=∠FBG,
∴∠EBP+∠CBG=∠BFP+∠FBG,
∴∠EBG=∠EGB,
∵BE⊥AF,
∴△BEG是等腰直角三角形.
(3)解:∵P是BC的中点,正方形的边长为4,
∴AB=4,BP=CP=2,
∵在Rt△ABP中,
∴AP=![]() ,
,
∵BE⊥AP,
∴S△ABP=![]() ,
,
解得:BE=![]() ,
,
∵AB=BC,AB=BF,
∴BC=BF,
由(1)可知∠CBG =∠FBG,
∴BG=BG,
∴△CBG≌△FBG,
∴∠BFP=∠BCG,
由(2)可知∠EBP=∠BFP,
∴∠EBP =∠BCG∵∠EPB =∠CPG,
∴△EBP≌△GCP,
∴CG=BE=![]() .
.
“点睛”本题考查正方形到现在、全等三角形的判定和性质、相等的垂直平分线的性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点 P(﹣3,2)绕原点 O 顺时针旋转 180°,所得到的对应点 P′的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
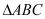 中,
中,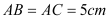 ,
,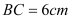 ,点D在BC边上运动,作
,点D在BC边上运动,作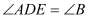 ,DE交AC于E。
,DE交AC于E。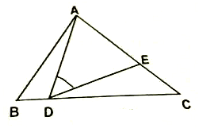
(1)求证:
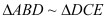 ;
;(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=2,则代数式2a﹣2b﹣3的值是( )
A.1
B.2
C.5
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个非零有理数a,b,规定:ab=ab-(a+b).若2(x+1)=1,则x的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的种类
②去图书馆收集学生借阅图书的记录
③绘制扇形图来表示各个种类所占的百分比
④整理借阅图书记录并绘制频数分布表
正确统计步骤的顺序是( )
A.②→③→①→④B.③→④→①→②C.①→②→④→③D.②→④→③→①
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线 C:y=x2先向左平移 2 个单位长度,然后再向上平移 1 个单位长度后,所得抛物线 C′的解析式为_________.
相关试题

