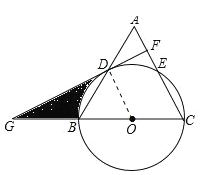
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由等腰三角形的性质证出∠A=∠ODB,得出OD∥AC,证出DF⊥OD,即可得出结论;
(2)证明△OBD是等边三角形,由等边三角形的性质得出∠BOD=60°,求出∠G=30°,由直角三角形的性质得出OG=2OD=2×6=12,由勾股定理得出DG的长,阴影部分的面积=△ODG的面积﹣扇形OBD的面积,即可得出答案.
试题解析:(1)证明:连接OD,如图所示:
∵AC=BC,OB=OD,∴∠ABC=∠A,∠ABC=∠ODB,∴∠A=∠ODB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∵OD是⊙O的半径,∴DF是⊙O的切线;
(2)解:∵AC=BC,∠A=60°,∴△ABC是等边三角形,∴ABC=60°,∵OD=OB,∴△OBD是等边三角形,∴∠BOD=60°,∵DF⊥OD,∴∠ODG=90°,∴∠G=30°,∴OG=2OD=2×6=12,∴DG=![]() OD=
OD=![]() ,∴阴影部分的面积=△ODG的面积﹣扇形OBD的面积=
,∴阴影部分的面积=△ODG的面积﹣扇形OBD的面积=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根是3a-2与4-a,则这个正数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设直线nx+(n+1)y=
 (n为自然数)与两坐标轴围成的三角形面积为Sn , 则S1+S2+…+S2016的值为
(n为自然数)与两坐标轴围成的三角形面积为Sn , 则S1+S2+…+S2016的值为 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线L1:y=k1x+b1 , L2:y=k2x+b2 , 若L1⊥L2 , 则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= x+3垂直,求解析式.
x+3垂直,求解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,正确的角度互化是( )
A.63.5°=63°50′B.23°12′36″=23.48°
C.18°18′18″=18.33°D.22.25°=22°15′
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
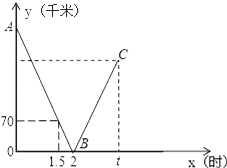
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)在(2)的条件下,若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.5a+3b=8abB.4a3+2a2=6a5
C.8b2﹣7b2=1D.6ab2﹣6b2a=0
相关试题

