【题目】把下列各数填在相应的大括号里(将各数用逗号分开):
+8,0.275,-|-2|,0,-1.04,-(-10),![]() ,
,![]() ,
,![]() ,0.1.
,0.1.
正整数:﹛ …﹜
整数:﹛ …﹜
负有理数: ﹛ …﹜
分数: ﹛ …﹜
参考答案:
【答案】正整数:﹛ +8,-(-10) ﹜
整数:﹛ +8,-(-10) ,0,-|-2|﹜
负有理数: ﹛ -|-2|,-1.04,![]() ﹜
﹜
分数: ﹛0.275,-1.04,0.1,![]() ,
,![]() ,
,![]() ﹜
﹜
【解析】
首先把有绝对值和有括号的数,去绝对值和去括号,然后先把整数和分数分开,然后在整数和分数里面对应的找到相应的数填在括号里面.
首先知道,-|-2|=-2,-(-10)=10
我们知道有理数分为整数和分数,
则整数有:+8,-(-10) ,0,-|-2|
分数有:0.275,-1.04,0.1,![]() ,
,![]() ,
,![]()
(除了无线不循环小数外,其它小数都可化为分数)
正整数即为整数里面的正数,+8,-(-10)(0既不是正数也不是负数,0是正负的分界点)
整数有+8,-(-10) ,0,-|-2|
负有理数即为负的整数和负的分数,-|-2|,-1.04,![]()
分数有0.275,-1.04,0.1,![]() ,
,![]() ,
,![]()
故答案为:
正整数:﹛ +8,-(-10) ﹜
整数:﹛ +8,-(-10) ,0,-|-2|﹜
负有理数: ﹛ -|-2|,-1.04,![]() ﹜
﹜
分数: ﹛0.275,-1.04,0.1,![]() ,
,![]() ,
,![]() ﹜
﹜
-
科目: 来源: 题型:
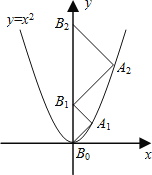
查看答案和解析>>【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=____
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数
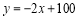 .
.(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式(利润=售价-制造成本);
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
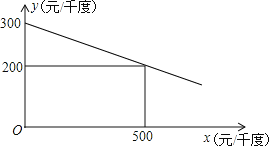
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.

(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求取近似数:
(1)2367890(精确到十万位);(2)29524(精确到千位);
(3)4.2046(精确到千分位);(4)3.102(精确到百分位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
 ,结果保留整数.)
,结果保留整数.)
相关试题

