【题目】某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数![]() .
.
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式(利润=售价-制造成本);
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
参考答案:
【答案】(1)z=-2x2+136x-1800(x>18);(2)当销售单价为34元时,每月能获得最大利润,最大利润是512万元.
【解析】
试题分析:(1)根据每月的利润z=(x-18)y,再把y=-2x+100代入即可求出z与x之间的函数解析式,
(2)把z=350代入z=-2x2+136x-1800,解这个方程即可,将z═-2x2+136x-1800配方,得z=-2(x-34)2+512,即可求出当销售单价为多少元时,厂商每月能获得最大利润,最大利润是多少.
试题解析:(1)z=(x-18)y=(x-18)(-2x+100)
=-2x2+136x-1800,
∴z与x之间的函数解析式为z=-2x2+136x-1800(x>18);
(2)由z=350,得350=-2x2+136x-1800,
解这个方程得x1=25,x2=43
所以,销售单价定为25元或43元,
将z=-2x2+136x-1800配方,得z=-2(x-34)2+512(x>18),
答;当销售单价为34元时,每月能获得最大利润,最大利润是512万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,体育老师对甲、乙两名同学每人进行10次立定跳远测试,他们的平均成绩相同,方差分别是S甲=0.20,S乙=0.16,则甲、乙两名同学成绩更稳定的是______.
-
科目: 来源: 题型:
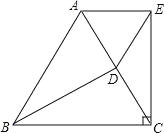
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年植树节,某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整)。
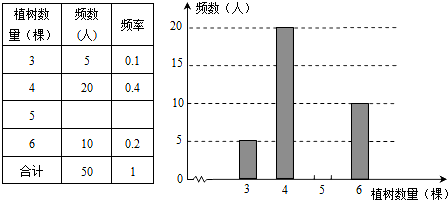
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数;并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:0,-1,7,1,x的平均数为1,则这组数据的极差是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC的两边长分别为2和5,则第三边长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A.20°或100°
B.120°
C.20°或120°
D.36°
相关试题

