【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
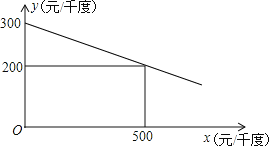
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
参考答案:
【答案】(1)工厂消耗每千度电产生利润是180元(2)当工厂每天消耗50千度电时,工厂每天消耗电产生利润为5000元
【解析】试题分析:(1)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可;
(2)根据利润=每天的用电量×每千度电产生利润y,然后整理得到W与m的关系式,再根据二次函数的最值问题解答.
解:(1)设工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b,
∵该函数图象过点(0,300),(500,200),
∴![]() ,
,
解得![]() .
.
所以y=﹣0.2x+300(x≥0),
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=﹣0.2×600+300=180(元/千度);
(2)设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(﹣0.2x+300)
=m[﹣0.2(5m+600)+300]
=﹣m2+180m
=﹣(m﹣90)2+8100,
在m≤90时,w随m的增大而最大,
由题意,m≤60,
∴当m=60时,w最大=﹣(60﹣90)2+8100=7200,
即当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y= -x2-2x的图象与x轴交于点A、O,在抛物线上有一点P,满足
S△AOP=3,则点P的坐标是( )
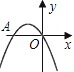
A. (-3,-3) B. (1,-3) C. (-3,-3)或(-3,1) D. (-3,-3)或(1,-3)
-
科目: 来源: 题型:
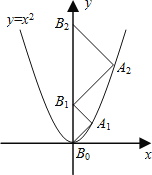
查看答案和解析>>【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=____
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数
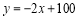 .
.(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式(利润=售价-制造成本);
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里(将各数用逗号分开):
+8,0.275,-|-2|,0,-1.04,-(-10),
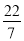 ,
,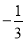 ,
,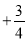 ,0.1.
,0.1.正整数:﹛ …﹜
整数:﹛ …﹜
负有理数: ﹛ …﹜
分数: ﹛ …﹜
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.

(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求取近似数:
(1)2367890(精确到十万位);(2)29524(精确到千位);
(3)4.2046(精确到千分位);(4)3.102(精确到百分位).
相关试题

