【题目】当m,n是正实数,且满足m+n=mn时,就称点P(m,![]() )为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=
)为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=![]() ,AM=4
,AM=4![]() ,求△MBC的面积
,求△MBC的面积
参考答案:
【答案】![]()
【解析】分析:由m+n=mn变式为![]() 可知P(m,m1),所以在直线y=x1上,点点A(0,5)在直线y=x+b上,求得直线AM:y=x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
可知P(m,m1),所以在直线y=x1上,点点A(0,5)在直线y=x+b上,求得直线AM:y=x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
详解:
∵m+n=mn且m,n是正实数,
∴![]() ,即
,即![]()
∴P(m,m1),
即“完美点”B在直线y=x1上,
∵点A(0,5)在直线y=x+b上,
∴b=5,
∴直线AM:y=x+5,
∵“完美点”B在直线AM上,
∴由![]() 解得
解得![]()
∴B(3,2),
∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=x,而直线y=x1与直线y=x平行,直线y=x+5与直线y=x平行,
∴直线AM与直线y=x1垂直,
∵点B是直线y=x1与直线AM的交点,
∴垂足是点B,
∵点C是“完美点”,
∴点C在直线y=x1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴![]()
∵![]()
∴![]()
又∵![]() ,
,
∴BC=1,
∴![]()
点睛:本题考查了一次函数的性质,直角三角形的判定,勾股定理的应用以及三角形面积的计算等,判断直线垂直,借助正比例函数是本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
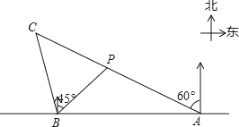
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段
 ,点
,点 在线段
在线段 上,当点
上,当点 是线段
是线段 和线段
和线段 的中点时,线段
的中点时,线段 的长为_________;若点
的长为_________;若点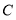 在线段
在线段 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段 与线段
与线段 之间的数量关系为_________.
之间的数量关系为_________. 
(2)应用:
如图3,现有长为40米的拔河比赛专用绳
 ,其左右两端各有一段(
,其左右两端各有一段( 和
和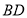 )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳 . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳 ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:①在图中标出点
 、点
、点 的位置,并简述画图方法;
的位置,并简述画图方法;②请说明①题中所标示
 点的理由.
点的理由. 
-
科目: 来源: 题型:
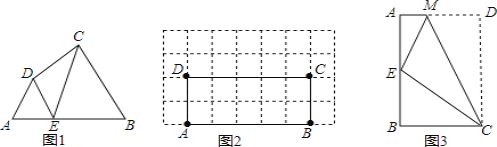
查看答案和解析>>【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 在△ABC中,AB=AC,Ac上的中线BD把△ABC的周长分为24cm和30cm两部分。求三角形的三边长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是 ( )

A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过
 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方 m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为 m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?
相关试题

