【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
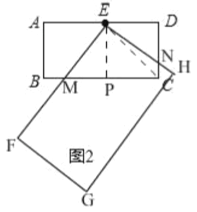
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 ![]() 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.


参考答案:
【答案】(1)证明见解析;(2)AM=BN;(3)EF 将边 BC 分成的两条线段的长度为![]() .
.
【解析】试题分析:(1)过点 E 作 ![]() ,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN=
,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN= ![]() PC,进而求出PN=CN=
PC,进而求出PN=CN=![]() ,再判断出AM=PN=
,再判断出AM=PN=![]() ,即可得出BM=
,即可得出BM=![]() ,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
试题解析:
(1) 如图1,过点 E 作 ![]() ,垂足为点 P,
,垂足为点 P,
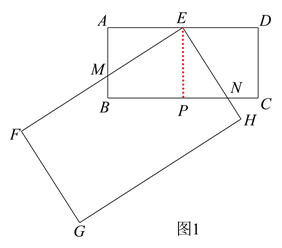
则四边形 ABPE 是矩形,∴PE=AB=1, ![]() ,
,
∵ 点 E 是 AD 的中点,∴![]() ,∴PE=AE,
,∴PE=AE,
∵![]() ,∴
,∴![]() ,
,
∵PE=AE, ![]() ,∴
,∴![]() ,∴EM=EN.
,∴EM=EN.
(2) 由(1)知, ![]() ,∴AM=PN,
,∴AM=PN,
∵AM=CN,∴PN=CN=![]() PC,
PC,
∵ 四边形 EPCD 是矩形,∴PC=DE=1,PN=CN=![]() ,
,
∴AM=PN=![]() ,BM=AB-AM=
,BM=AB-AM=![]() ,∴AM=BN.
,∴AM=BN.
(3)如图2,当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM=![]() ,
,
∴BM=BP﹣PM=1﹣![]() ,CM=PC+PM=1+
,CM=PC+PM=1+![]() ,
,
∴EF将边BC分成的两条线段的长度为1﹣![]() ,1+
,1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是( )
A. 冷水加热过程中小气泡上升并变为大气泡
B. 钟表上时针的运动
C. 风筝在空中飘动
D. 急刹车时汽车在地面上滑行
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以下图形中,是中心对称图形的是( )
A.等边三角形
B.等腰梯形
C.平行四边形
D.正五边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】平移是图形的变换,许多汉字也可以看成是由字中的一部分平移得到的,如“晶、森”等.请你开动脑筋,写出至少三个可以由平移变换得到的字(与题中举例不同):__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:① △ODC是等边三角形;②BC=2AB;③∠AOE=135°; ④S△AOE=S△COE,其中正确的结论的个数有
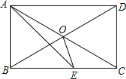
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】|﹣16|的算术平方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)2a2﹣8
(2)(x﹣1)2﹣2(x﹣1)﹣3
相关试题

