【题目】在四边形ABCD中,AB∥CD,∠BCD=90o,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段
DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).
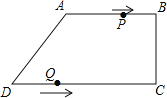
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
参考答案:
【答案】(1)16cm(2)(8+8![]() )cm(3)当t=
)cm(3)当t=![]() 秒或
秒或![]() 秒时,△BPQ的面积为20cm2
秒时,△BPQ的面积为20cm2
【解析】试题分析:(1)过A作AM⊥DC于M,得出平行四边形AMCB,求出AM,根据勾股定理求出DM即可;
(2)根据平行四边形的对边相等得出方程,求出即可;
(3)分为三种情况,根据题意画出符合条件的所有图形,根据三角形的面积得出方程,求出符合范围的数即可.
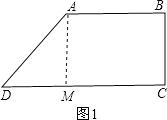
试题解析:(1)如图1,过A作AM⊥DC于M,
∵在四边形ABCD中,AB∥CD,∠BCD=90°,
∴AM∥BC,
∴四边形AMCB是矩形,
∵AB=AD=10cm,BC=8cm,
∴AM=BC=8cm,CM=AB=10cm,
在Rt△AMD中,由勾股定理得:DM=6cm,
CD=DM+CM=10cm+6cm=16cm;
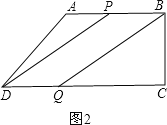
(2)如图2,当四边形PBQD是平行四边形时,PB=DQ,
即10-3t=2t,
解得t=2,
此时DQ=4,CQ=12,BQ=![]() =4
=4![]() ,
,
所以C□PBQD=2(BQ+DQ)=8+8![]() ;
;
即四边形PBQD的周长是(8+8![]() )cm;
)cm;
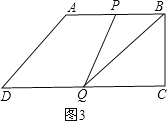
(3)当P在AB上时,如图3,
即0≤t≤![]() ,
,
S△BPQ=![]() BPBC=4(10-3t)=20,
BPBC=4(10-3t)=20,
解得t=![]() ;
;
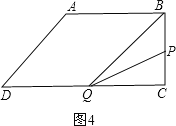
当P在BC上时,如图4,即![]() <t≤6,
<t≤6,
S△BPQ=![]() BPCQ=
BPCQ=![]() (3t-10)(16-2t)=20,、
(3t-10)(16-2t)=20,、
此方程没有实数解;
当P在CD上时:
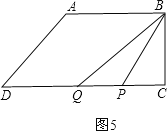
若点P在点Q的右侧,如图5,即6<t≤![]() ,
,
S△BPQ=![]() PQBC=4(34-5t)=20,
PQBC=4(34-5t)=20,
解得t=![]() <6,不合题意,应舍去;
<6,不合题意,应舍去;
若P在Q的左侧,如图6,即![]() <t≤8,
<t≤8,

S△BPQ=![]() PQBC=4(5t-34)=20,
PQBC=4(5t-34)=20,
解得t=![]() ;综上所述,当t=
;综上所述,当t=![]() 秒或
秒或![]() 秒时,△BPQ的面积为20cm2.
秒时,△BPQ的面积为20cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 与y=mx﹣m(m≠0)在同一平面直角坐标系中的图象可能是( )
与y=mx﹣m(m≠0)在同一平面直角坐标系中的图象可能是( )
A.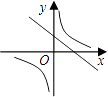
B.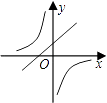
C.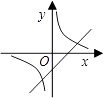
D.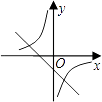
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足
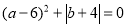 .
.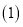 写出a、b及AB的距离:
写出a、b及AB的距离: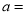 ______
______ 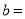 ______
______ 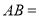 ______
______ 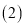 若动点P从点A出发,以每秒6个单位长度沿数轴向左匀速运动,动点Q从点B出发,以每秒4个单位长度向左匀速运动.
若动点P从点A出发,以每秒6个单位长度沿数轴向左匀速运动,动点Q从点B出发,以每秒4个单位长度向左匀速运动. 若P、Q同时出发,问点P运动多少秒追上点Q?
若P、Q同时出发,问点P运动多少秒追上点Q?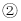 若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.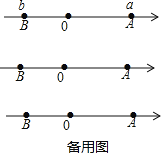
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果某一年的7月份中,有4个星期六,它们的日期之和为70,那么这个月的18日是星期 _____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是三角形的三条边,则|a+b﹣c|﹣|c﹣a﹣b|的化简结果为( )
A. 0 B. 2a+2b C. 2c D. 2a+2b﹣2c
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=﹣0.22 , b=﹣2﹣2 , c=(﹣
 )﹣2 , d=(﹣
)﹣2 , d=(﹣  )0 , 将a,b,c,d按从大到小的关系排列 .
)0 , 将a,b,c,d按从大到小的关系排列 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.从同一点引出的两条射线组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.两条有公共端点的线段组成的图形叫角
相关试题

