【题目】如图,已知直线AB:y=![]() x+
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )

A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
参考答案:
【答案】A
【解析】
作EF⊥BC于F,设AD=EC=x.利用勾股定理可得BD+BE=![]() +
+![]() =
=![]() +
+![]() ,要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到G(
,要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到G(![]() ,3),K(
,3),K(![]() ,
,![]() )的距离之和最小.
)的距离之和最小.
解:由题意A(0,![]() ),B(-3,0),C(3,0),
),B(-3,0),C(3,0),
∴AB=AC=8,
作EF⊥BC于F,设AD=EC=x.

∵EF∥AO,
∴![]() ,
,
∴EF=![]() ,CF=
,CF=![]() ,
,
∵OH∥EF,
∴![]() ,
,
∴OH=![]() ,
,
∴BD+BE=![]() +
+![]() =
=![]() +
+![]() ,
,
要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到K(![]() ,3),G(
,3),G(![]() ,
,![]() )的距离之和最小.
)的距离之和最小.

设G关于x轴的对称点G′(![]() ,
,![]() ),直线G′K的解析式为y=kx+b,
),直线G′K的解析式为y=kx+b,
则有 ,
,
解得k=![]() ,b=
,b=![]() ,
,
∴直线G′K的解析式为y=![]() x
x![]() ,
,
当y=0时,x=![]() ,
,
∴当x=![]() 时,MG+MK的值最小,此时OH=
时,MG+MK的值最小,此时OH=![]() =
=![]() =4,
=4,
∴当BD+BE的值最小时,则H点的坐标为(0,4),
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2 m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为( )
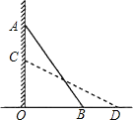
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCD、正方形A1CC1D1、正方形A2C1C2D2的顶点A、A1、A2和O、C、C1、C2分别在一次函数y=x+1的图象和x轴上,若正比例函数y=kx则过点D5,则系数k的值是( )
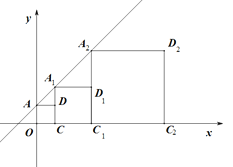
A.
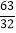 B.
B. 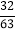 C.
C. 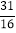 D.
D. 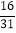
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
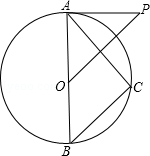
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP=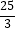 ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元? -
科目: 来源: 题型:
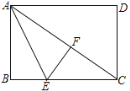
查看答案和解析>>【题目】如图,已知矩形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上.若BE=3,EC=5,则AB的长为_____.
相关试题

