【题目】如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2 m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为( )
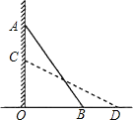
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
参考答案:
【答案】A
【解析】
设BO=xm,利用勾股定理用x表示出AB和CD的长,根据AB=CD列出方程求出x的值,即可求出AB的长度.
设BO=xm,依题意,得AC=0.5m,BD=0.5m,AO=2m.
在Rt△AOB中,根据勾股定理得
AB2=AO2+OB2=22+x2,
在Rt△COD中,根据勾股定理
CD2=CO2+OD2=(2-0.5)2+(x+0.5)2,
∴22+x2=(2-0.5)2+(x+0.5)2,
解得x=1.5,
∴AB=![]() =2.5m,
=2.5m,
答:梯子AB的长为2.5m.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为
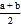 .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为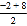 =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCD、正方形A1CC1D1、正方形A2C1C2D2的顶点A、A1、A2和O、C、C1、C2分别在一次函数y=x+1的图象和x轴上,若正比例函数y=kx则过点D5,则系数k的值是( )
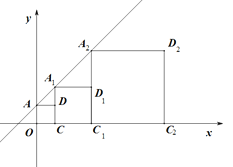
A.
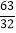 B.
B. 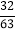 C.
C. 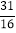 D.
D. 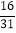
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB:y=
 x+
x+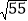 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
A. (0,4) B. (0,5) C. (0,
 ) D. (0,
) D. (0,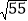 )
)
相关试题

