【题目】发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
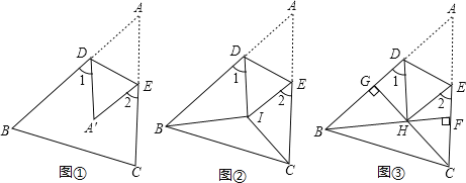
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
参考答案:
【答案】(1)∠1+∠2=2∠A;理由见解析;(2)∠BIC=115°;(3)∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).
【解析】
(1)根据翻折变换的性质、三角形内角和定理、以及平角的定义求出即可;
(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°-![]() ∠A,在用三角形的内角和定理即可求出∠BIC的度数可;
∠A,在用三角形的内角和定理即可求出∠BIC的度数可;
(3)根据垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,再依据四边形AGHF的内角和为360°,表示出![]() 与
与![]() 的关系,运用对顶角等量代换,得到
的关系,运用对顶角等量代换,得到![]() 与
与![]() 的关系,再结合第(1)问,得到∠BHC与∠1+∠2的关系.
的关系,再结合第(1)问,得到∠BHC与∠1+∠2的关系.
解:(1)∠1+∠2=2∠A;
理由:根据翻折的性质,∠ADE=![]() (180°-∠1),∠AED=
(180°-∠1),∠AED=![]() (180°-∠2),
(180°-∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+![]() (180-∠1)+
(180-∠1)+![]() (180-∠2)=180°,
(180-∠2)=180°,
整理得2∠A=∠1+∠2;
(2)![]() 由(1)知:∠1+∠2=2∠A,
由(1)知:∠1+∠2=2∠A,
又![]() ∠1+∠2=100°,
∠1+∠2=100°,
∴∠A=50°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A=90°+
∠A=90°+![]() ×50°=115°;
×50°=115°;
(3)∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,
∴∠FHG+∠A=180°,
∴∠BHC=∠FHG=180°-∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).
-
科目: 来源: 题型:
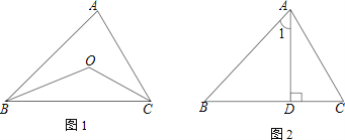
查看答案和解析>>【题目】(1)如图1,△ABC中,∠BAC=60°,内角∠ABC、∠ACB的平分线相交于点O,则∠BOC=______;
(2)如图2,△ABC中,∠BAC=60°,AD是△ABC的边BC上的高,且∠B=∠1,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=﹣
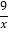 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=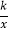 上运动,则k的值为( )
上运动,则k的值为( )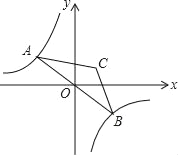
A. 3 B. 4 C. 2.5 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长BE=20cm,宽AB=10cm,高AD=15cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
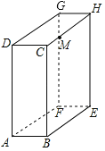
A.
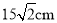 B.
B. 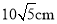
C.
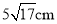 D.
D. 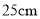
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上
 、
、 、
、 三点所代表的数分别是
三点所代表的数分别是 、
、 、
、 ,且
,且 .若下列选项中,有一个表示
.若下列选项中,有一个表示 、
、 、
、 三点在数轴上的位置关系,则此选项为何?( )
三点在数轴上的位置关系,则此选项为何?( )A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将挂好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为320cm,在无风的天气里,彩旗自然下垂,如图所示,
(1)求彩旗下垂时最低处离地面的最小高度h.彩旗完全展平时的尺寸如图的长方形(单位:cm)
(2)商店彩旗的标价为每面40元,旗杆的标价为每根20元,学校计划购买彩旗60面,旗杆50根,由于数量较多商店决定给予学校优惠,其中彩旗每面优惠10%,旗杆每根优惠
 a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.
a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O。
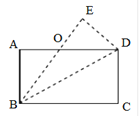
(1)由折叠可知△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请写出其他一组全等三角形__________________.
(2)图中有等腰三角形吗?请你找出来__________________.
(3)若AB=6,BC=8,求OB的长度。
相关试题

