搜索
【题目】如图所示，已知MN⊥PQ于点O，点A、 
是以MN为轴的对称点，而点 
、A是以PQ为轴的对称点，求证：点 、 是以点O为对称中心的对称点．
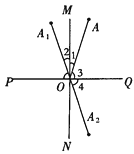
参考答案：
【答案】证明：∵点A、 
关于MN轴对称，∴OA＝ 
，∠1＝∠2，同理OA＝ 
，∠3＝∠4，∴ ＝ ，∠1＋∠2＋∠3＋∠4＝2（∠1＋∠3）＝180°，∴点 、 
是以点O为对称中心的对称点．
【解析】中心对称的性质：对称点所连线段都经过对称中心，而且被对称中心所平分．
【考点精析】本题主要考查了中心对称及中心对称图形的相关知识点，需要掌握如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：抛物线y=ax2＋bx＋c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC＋OD，
（1）求抛物线的解析式；
（2）设点P（x,y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，写出自变量x的取值范围,并求当x取多少时，S的值最大，最大是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′ ，如图①所示，∠BAB′ ＝θ，
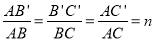，我们将这种变换记为[θ，n] ．（1）如图①，对△ABC作变换[60°，
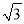]得到△AB′C′ ，则
:
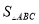= ；直线BC与直线B′C′所夹的锐角为 度； （2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、
在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．
-
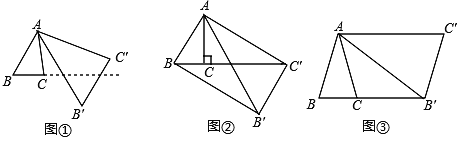
科目： 来源： 题型：
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元，已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次采购的数量是第一次采购数量的两倍.
（1）试问去年每吨大蒜的平均价格是多少元？
（2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元.为出口需要，所有采购的大蒜必须在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角三角板ABC的斜边AB=12cm，∠A=30°，将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使点B′落在原三角板ABC的斜边AB上，则三角板A′B′C′平移的距离为（ ）
A.6cm
B.（6﹣2
）cm
C.3cm
D.（4﹣6）cm -
科目： 来源： 题型：
查看答案和解析>>【题目】2018年12月有5个星期一，它们的日期之和为85，那么这个月的5号是星期（ ）
A. 一 B. 二 C. 三 D. 四
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂一种产品的年产量是20件，如果每一年都比上一年的产品增加x倍，两年后产品y与x的函数关系是（ ）
A.y=20（1﹣x）2
B.y=20+2x
C.y=20（1+x）2
D.y=20+20x2+20x
相关试题
