【题目】对于未知数为 x,y 的二元一次方程组,如果方程组的解 x,y 满足![]() ,我们就说方程组的解 x 与 y 具有“邻好关系”.
,我们就说方程组的解 x 与 y 具有“邻好关系”.
(1) 方程组![]() 的解x与y是否具有“邻好关系”? 说明你的理由;
的解x与y是否具有“邻好关系”? 说明你的理由;
(2) 若方程组![]() 的解x与y具有“邻好关系”,求m的值;
的解x与y具有“邻好关系”,求m的值;
(3) 未知数为x,y的方程组![]() ,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
参考答案:
【答案】(1)方方程组的解x,y具有“邻好关系” ;(2)m=6或m=4;(3)a=1,方程组的解为![]() .
.
【解析】
(1)先求出方程组![]() 的解,再根据“邻好关系”的定义判断即可;
的解,再根据“邻好关系”的定义判断即可;
(2)用含m的代数式表示出方程组![]() 的解,然后根据
的解,然后根据![]() 列方程求解;
列方程求解;
(3)用含a的代数式表示出方程组![]() 的解,然后根据a与x,y都是正整数讨论即可.
的解,然后根据a与x,y都是正整数讨论即可.
(1)![]()
①-②,得
3y=6,
∴y=2,
把y=2代入①得,
x+4=7,
∴x=3,
∴方程组解得![]() ,
,
∵![]() ,
,
∴方程组的解x,y具有“邻好关系”.
(2)方程组解得![]() ,
,
![]() ,
,
∴5-m=±1,
∴m=6或m=4 ;
(3) ![]() ,
,
①+②得:![]() ,
,
∴![]() ③,
③,
把③代入②得
![]() ,
,
∴![]() ,
,
∵a,x,y均为正整数,
∴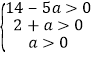 ,
,
∴![]() ,
,
∴当a=1时, x=3,y=4;
当a=2时,x=1,y=3;
在上面符合题意的两组解中,只有a=1时,|3-4|=1,
∴a=1,该方程组的解x与y具有“邻好关系”,此时方程组的解为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.

请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
-
科目: 来源: 题型:
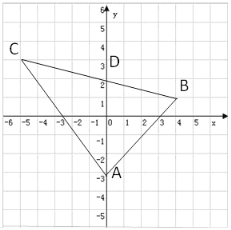
查看答案和解析>>【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 分别是边
分别是边 上的点,
上的点, 和
和 交于点
交于点 ,且
,且 .
.(1)如图
 ,求证:
,求证: ;
;(2)如图
 ,过点
,过点 作
作 ,交
,交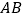 于点
于点
 ,求证
,求证 ;
;(3)如图
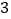 ,在(2)的条件下,
,在(2)的条件下, ,求线段
,求线段 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2
 ,∠DCF=30°,则EF的长为( )
,∠DCF=30°,则EF的长为( )
A.4
B.6
C.
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )

A.②④
B.①④
C.①③
D.②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且
 .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.

相关试题

