【题目】在![]() 中,
中,![]() 分别是边
分别是边![]() 上的点,
上的点,![]() 和
和![]() 交于点
交于点![]() ,且
,且![]() .
.
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]()
![]() ,求证
,求证![]() ;
;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() ,求线段
,求线段![]() 的长.
的长.

参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据三角形内角和定理可得∠ECF+∠CFE+∠CEF=180°,![]() ,由
,由![]() 且
且![]() 是公共角即可证明
是公共角即可证明![]() (2)根据锐角互余的关系可得
(2)根据锐角互余的关系可得![]() ,根据
,根据![]() 及外角性质可得∠CAB=∠CGA,进而可得AC=CG;(3)过点
及外角性质可得∠CAB=∠CGA,进而可得AC=CG;(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() 进而可得AG=2MC,由∠HAB=90°,∠CAB=45°可得
进而可得AG=2MC,由∠HAB=90°,∠CAB=45°可得![]() 平分
平分![]() ,由
,由![]() 可得CM=CN,根据四边形内角和及平角的定义可得
可得CM=CN,根据四边形内角和及平角的定义可得![]() ,利用AAS可证明△HNC≌△CMD,即可证明CD=CH,根据已知即可证明AE=HE,根据(1)得
,利用AAS可证明△HNC≌△CMD,即可证明CD=CH,根据已知即可证明AE=HE,根据(1)得![]() ,由
,由![]() 可得∠AEC=∠H,可得AE=AH,进而可得
可得∠AEC=∠H,可得AE=AH,进而可得![]() ,在
,在![]() 中,
中,![]() 可得∠B=30°,根据含30°角的直角三角形性质可知
可得∠B=30°,根据含30°角的直角三角形性质可知![]() ,根据面积公式可得
,根据面积公式可得![]() ,即可求出CM的值,进而根据
,即可求出CM的值,进而根据![]() 可得BC的长.
可得BC的长.
(1)在![]() 中,∠ECF+∠CFE+∠CEF=180°,
中,∠ECF+∠CFE+∠CEF=180°,
在![]() 中,
中,![]()
![]() 且
且![]() 是公共角
是公共角
∴∠CEF=∠CDB
即![]()
(2)![]() ,
,
∴∠DCB=∠ACG=90°,
∴![]()
即![]()
∵∠ACD+∠B=∠CAB,
∴∠GCB+∠B=∠CAB,
∵∠CGA=∠GCB+∠B,
∴∠CAB=∠CGA,
∴AC=GC
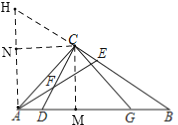
(3)如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]()
![]() 且
且![]()
∴∠CAG=∠CGA=45°,![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∵![]()
∴![]() ,
,
∵∠CAG=45°,
∴∠CAH=∠CAG,
![]() 平分
平分![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在四边形![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴AE=AH,
∵![]() ,CM=CN,∠HNC=∠CMD,
,CM=CN,∠HNC=∠CMD,
∴△HNC≌△CMD,
∴CD=CH,
∵CE+CD=AE,
∴CE+CH=AE=EH
∴AE=EH=HA,
∴∠H=60°,
在![]() 中,
中,![]()
∴∠B=30°,
在![]() 中,
中,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
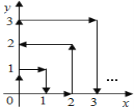
查看答案和解析>>【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳动一个单位长度,那么30秒后跳蚤所在位置的坐标是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.

请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
-
科目: 来源: 题型:
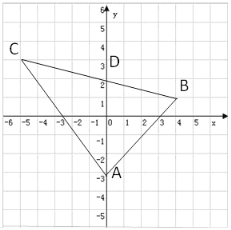
查看答案和解析>>【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于未知数为 x,y 的二元一次方程组,如果方程组的解 x,y 满足
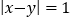 ,我们就说方程组的解 x 与 y 具有“邻好关系”.
,我们就说方程组的解 x 与 y 具有“邻好关系”.(1) 方程组
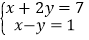 的解x与y是否具有“邻好关系”? 说明你的理由;
的解x与y是否具有“邻好关系”? 说明你的理由;(2) 若方程组
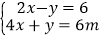 的解x与y具有“邻好关系”,求m的值;
的解x与y具有“邻好关系”,求m的值;(3) 未知数为x,y的方程组
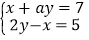 ,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2
 ,∠DCF=30°,则EF的长为( )
,∠DCF=30°,则EF的长为( )
A.4
B.6
C.
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )

A.②④
B.①④
C.①③
D.②③
相关试题

