【题目】直线y=﹣x+6与x轴交于A,与y轴交于B,直线CD与y轴交于C(0,2)与直线AB交于D,过D作DE⊥x轴于E(3,0). 
(1)求直线CD的函数解析式;
(2)P是线段OA上一动点,点P从原点O开始,每秒一个单位长度的速度向A运动(P与O,A不重合),过P作x轴的垂线,分别与直线AB,CD交于M,N,设MN的长为S,P点运动的时间为t,求出S与t之间的函数关系式(写出自变量的取值范围)
(3)在(2)的条件下,当t为何值时,以M,N,E,D为顶点的四边形是平行四边形.(直接写出结果)
参考答案:
【答案】
(1)解:∵直线CD与y轴相交于(0,2),
∴可设直线CD解析式为y=kx+2,
把x=3代入y=﹣x+6中可得y=3,
∴D(3,3),
把D点坐标代入y=kx+2中可得3=3k+2,解得k= ![]() ,
,
∴直线CD的函数解析式为y= ![]() x+2;
x+2;
(2)解:由题意可知OP=t,
把x=t代入y=﹣x+6中可得y=﹣t+6,
∴M(t,﹣t+6),
把x=t代入y= ![]() x+2中可得y=
x+2中可得y= ![]() t+2,
t+2,
∴N(t, ![]() t+2),
t+2),
∴MN=|﹣t+6﹣( ![]() t+2)|=|﹣
t+2)|=|﹣ ![]() +4|,
+4|,
∵点P在线段OA上,且A(6,0),
∴0<t<6;
(3)解:由题意可知MN∥DE,
∵以M,N,E,D为顶点的四边形是平行四边形,
∴MN=DE=3,
∴|﹣ ![]() +4|=3,解得t=
+4|=3,解得t= ![]() 或t=
或t= ![]() ,
,
即当t的值为 ![]() 或
或 ![]() 时,以M,N,E,D为顶点的四边形是平行四边形.
时,以M,N,E,D为顶点的四边形是平行四边形.
【解析】(1)由条件可先求得D点坐标,再利用待定系数法可求得直线CD的函数解析式;(2)用t可分别表示出M、N的坐标,则可表示出S与t之间的关系式;(3)由条件可知MN∥DE,利用平行四边形的性质可知MN=DE,由(2)的关系式可得到关于t的方程,可求得t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(3x+2y+1)2﹣(3x+2y﹣1)(3x+2y+1)
-
科目: 来源: 题型:
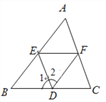
查看答案和解析>>【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x﹣1)(x﹣3)=0的解为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数-5,0,3中,最小的数是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,如果∠A:∠B:∠C=1:1:2,那么它是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
相关试题

