【题目】在直角墙角AOB(OA⊥OB,且OA,OB长度不限)中.要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 . 
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
参考答案:
【答案】
(1)
解:设BC的长为xm,则AC的长为(20-x)m;
由题意得(20-x)x=96,
整理得x2-20x+96=0,
解得x1=4,x2=24(舍去),
则AC的长为16m。
(2)
解:96÷(0.8×0.8)×55=8250(元);
96÷(1×1)×80=7680(元);
因为8250<7680,
所以用1.00×1.00(单位:m)的地板砖的费用较少。
【解析】(1)列一元二次方程解答,已知矩形的面积,可设其中一条边为x,用x表示另外一条边,列出方程解出x的值,并根据实际取x的值,写出矩形的长;(2)总面积÷一块的面积=用的块数,用的块数×单价=费用。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015秋永登县期末)下列去括号中,正确的是( )
A. a﹣(b﹣c)=a﹣b﹣c
B. c+2(a﹣b)=c+2a﹣b
C. a﹣(b﹣c)=a+b﹣c
D. a﹣(b﹣c)=a﹣b+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根。并求以此两根为边长的直角三角形的周长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2015+a2016的值为 .
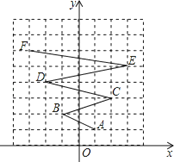
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形。.

(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是等邻边四边形。请写出你添加的一个条件;
(2)问题探究
小明猜想:对角线互相平分的等邻边四边形是菱形.她的猜想正确吗?请说明理由.
如图2,小明面了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,井将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.小明要是平移后的四边形ABC′A′是“等邻边四边形”应平移多少距离(即线段BB′的长)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
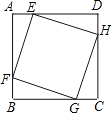
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.

(1)可求得x= .
(2)第2017个格子中的数为 ;
(3)前n个格子中所填整数之和是否可能为2020?若能,求出n的值,若不能,请说明理由;
相关试题

