【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x﹣c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.
参考答案:
【答案】
(1)
解:点B(0,2)向上平移6个单位得到点B'(0,8),
将A(4,0),B'(0,8)分别代入y=ax2+2x﹣c,得
![]() ,
,
解得 ![]() ,
,
∴原抛物线为y=﹣x2+2x+8,向下平移6个单位后所得的新抛物线为y=﹣x2+2x+2,
∴顶点C的坐标为(1,3)
(2)
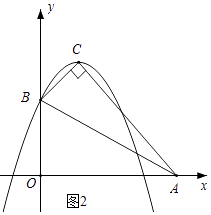
解:如图2,由A(4,0),B(0,2),C(1,3),得
AB2=20,AC2=18,BC2=2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴tan∠CAB= ![]() =
= ![]() =
= ![]() ;
;
(3)
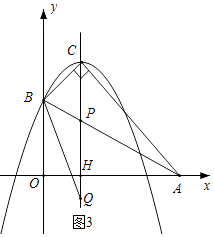
解:如图3,设抛物线的对称轴x=1与x轴交于点H,
由 ![]() =
= ![]() =
= ![]() ,得PH=
,得PH= ![]() AH=
AH= ![]() ,
,
∴P(1, ![]() ),
),
由HA=HC=3,得∠HCA=45°,
∴当点Q在点C下方时,∠BCQ=∠ACP,
因此△BCQ与△ACP相似分两种情况:
①如图3,当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,
,
解得CQ=4,
此时Q(1,﹣1);
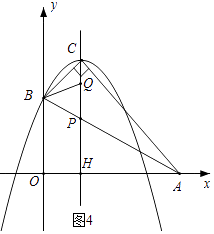
②如图4,当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,
,
解得CQ= ![]() ,
,
此时Q(1, ![]() ).
).
【解析】(1)先根据点B(0,2)向上平移6个单位得到点B'(0,8),将A(4,0),B'(0,8)分别代入y=ax2+2x﹣c,得原抛物线为y=﹣x2+2x+8,向下平移6个单位后所得的新抛物线为y=﹣x2+2x+2,据此求得顶点C的坐标;(2)根据A(4,0),B(0,2),C(1,3),得到AB2=20,AC2=18,BC2=2,进而得出AB2=AC2+BC2 , 根据∠ACB=90°,求得tan∠CAB的值即可;(3)先设抛物线的对称轴x=1与x轴交于点H,根据 ![]() =
= ![]() =
= ![]() ,求得PH=
,求得PH= ![]() AH=
AH= ![]() ,进而得到P(1,
,进而得到P(1, ![]() ),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
【考点精析】利用二次函数的概念和二次函数的图象对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
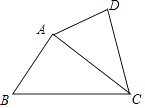
A.∠DAC=∠ABC
B.AC是∠BCD的平分线
C.AC2=BC?CD
D.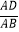 =
= 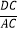
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,且过△ABC的重心,分别与AB,AC交于点D,E,点P是线段DE上一点,CP的延长线交AB于点Q,如果
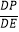 =
=  ,那么S△DPQ:S△CPE的值是 .
,那么S△DPQ:S△CPE的值是 . 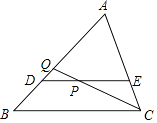
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,AB=10,sinB=
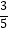 ,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.
,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.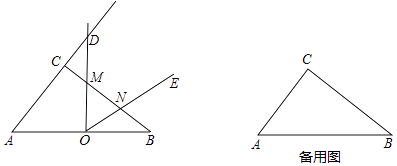
(1)当CM=2时,求线段CD的长;
(2)设CM=x,BN=y,试求y与x之间的函数解析式,并写出定义域;
(3)如果△OMN是以OM为腰的等腰三角形,请直接写出线段CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠BAD=∠CDA,AB=DC=
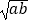 ,CE=a,AC=b,求证:
,CE=a,AC=b,求证: 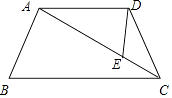
(1)△DEC∽△ADC;
(2)AEAB=BCDE. -
科目: 来源: 题型:
查看答案和解析>>【题目】一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)
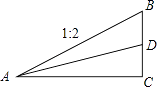
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知向量
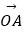 ,
, 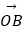 ,
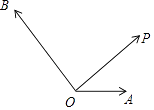
, 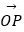 .
. 
(1)求做:向量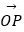 分别在
分别在 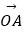 ,
, 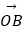 方向上的分向量
方向上的分向量  ,
, 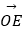 :(不要求写作法,但要在图中明确标出向量
:(不要求写作法,但要在图中明确标出向量  和
和 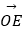 ).
).
(2)如果点A是线段OD的中点,联结AE、交线段OP于点Q,设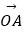 =
=  ,
, 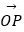 =
= 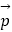 ,那么试用
,那么试用  ,
, 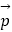 表示向量
表示向量 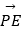 ,
, 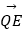 (请直接写出结论)
(请直接写出结论)
相关试题

