【题目】已知函数![]() ,画出图象并根据函数图象回答下列问题:
,画出图象并根据函数图象回答下列问题:
(1)列表、描点、连线
x | |||||
|
(2)![]() 的两个解是多少?
的两个解是多少?
(3)x取何值时,y>0?
(4)x取何值时,抛物线在x轴上或下方?
(5)抛物线![]() 与直线y=k有唯一的交点,则k= .
与直线y=k有唯一的交点,则k= .

参考答案:
【答案】(1)答案见解析;(2)x1=2、x2=6;(3)当x<2或x>6时;(4)当2≤x≤6时,抛物线在x轴上或下方;(5)﹣2.
【解析】试题分析: (1)完成表格、画出函数图象,根据抛物线与x轴交点横坐标即为该方程的解即可得;
(2)根据函数图象位于x轴上方部分对应的x的范围即为y>0的解集可得;
(3)由抛物线位于x轴上或下方部分所对应的x的范围即可得;
(4)由直线y=﹣2与抛物线有唯一交点可得答案.
试题解析:
解:(1)函数图象如下:
x | 1 | 2 | 3 | 4 | 6 |
y= |
| 0 | ﹣ | 2 | 0 |
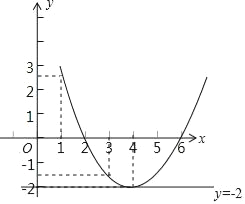
由函数图象可知, ![]() ﹣4x+6=0的两个解是x1=2、x2=6;
﹣4x+6=0的两个解是x1=2、x2=6;
(2)当x<2或x>6时,y>0;
(3)当2≤x≤6时,抛物线在x轴上或下方;
(4)由图可知,直线y=﹣2与抛物线只有唯一交点,
∴k=﹣2,
故答案为:﹣2.
-
科目: 来源: 题型:
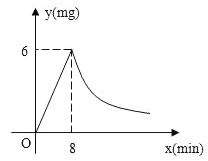
查看答案和解析>>【题目】为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
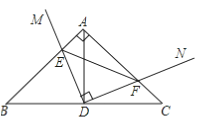
A. ①②④ B. ②③④
C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
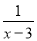 -2=
-2=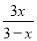 ;
;(2)设y=kx,且k≠0,若代数式(x-3y)(2x+y)+y(x+5y)化简的结果为2x2,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知a+b=7,ab=10,求a2+b2,(a-b)2的值;
(2)先化简(
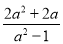 -
-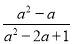 )÷
)÷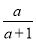 ,并回答:原代数式的值可以等于-1吗?为什么?
,并回答:原代数式的值可以等于-1吗?为什么? -
科目: 来源: 题型:
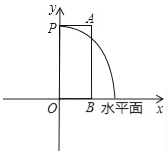
查看答案和解析>>【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
相关试题

