搜索
【题目】如图，在边长为1个单位长度的小正方形组成的网格中．
（1）画图：平移三角形ABC至三角形
，使点A与A对应.
（2）线段AB与
的位置关系是________.
（3）求
的面积．
参考答案：
【答案】（1）如图，
为所求,见解析；（2）
；（3）
3.5．
【解析】
（1）先由A和
得到平移的规则，再根据平移的性质得到
和
，连接、、即可得到答案；
（2）根据平移的性质即可得到线段AB与
的位置关系；
（3）用割补法进行计算即可得到答案.
（1）由题意可知A先向上平移4个单位，再向右平移5个单位得到，则可根据平移的性质得到和，连接、、，如图，为所求;
（2）因为三角形ABC平移得到三角形
，根据平移的性质即可得到.
（3）
=9-3-1.5-1，
=9-5.5，
=3.5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，
，
，
，
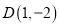．把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A-B-C-D-A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，天星山山脚下西端A处与东端B处相距800(1＋
)米，小军和小明同时分别从A处和B处向山顶C匀速行走．已知山的西端的坡角是45°，东端的坡角是30°，小军的行走速度为
米/秒．若小明与小军同时到达山顶C处，则小明的行走速度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点 A（﹣2，0），B（2，0），C（0，2），点 D，点E分别是 AC，BC的中点，将△CDE绕点C逆时针旋转得到△CD′E′，及旋转角为α，连接 AD′，BE′．
（1）如图①，若 0°＜α＜90°，当 AD′∥CE′时，求α的大小；
（2）如图②，若 90°＜α＜180°，当点 D′落在线段 BE′上时，求 sin∠CBE′的值；
（3）若直线AD′与直线BE′相交于点P，求点P的横坐标m的取值范围（直接写出结果即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题9分）把代数式通过配凑等手段，得到完全平方式，再运用完全平方式是非负性这一性质增加问题的条件，这种解题方法叫做配方法．配方法在代数式求值，解方程，最值问题等都有着广泛的应用．
例如：①用配方法因式分解：a2+6a+8
原式=a2+6a+9－1
=（a+3）2 –1
=（a+3－1）（a+3+1）
=（a+2）（a+4）
②若M=a2－2ab+2b2－2b+2，利用配方法求M的最小值：
a2－2ab+2b2－2b+2=a2－2ab+b2+b2－2b+1+1
=（a－b）2+（b－1）2 +1
∵（a－b）2≥0，（b－1）2 ≥0
∴当a=b=1时，M有最小值1
请根据上述材料解决下列问题：
（1）在横线上添上一个常数项使之成为完全平方式：a 2+4a+ ．
（2）用配方法因式分解： a2－24a+143
（3）若M=
a2+2a +1，求M的最小值．（4）已知a2+b2+c2－ab－3b－4c+7=0，求a+b+c的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB，CD边于点E，F.
（1）求证：四边形DEBF是平行四边形；
（2）当四边形DEBF是菱形时，求菱形的周长．
（3）在（2）的基础上，直接写出BD与EF的位置关系．
-
科目： 来源： 题型：
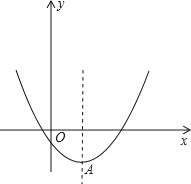
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx+4m﹣8,
（1）当x≤2时，函数值y随x的增大而减小，求m的取值范围．
（2）以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN（M，N两点在拋物线上），请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由．
（3）若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数，求整数m的最小值．
相关试题
