【题目】如图,![]() ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图,若点D为线段AC的中点,求证:AD=CE;
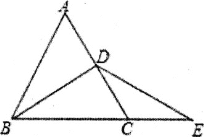
(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等边三角形三线合一的性质即可求得∠DBC的度数,根据BD=DE即可解题;
(2)作DF∥AB,可证△BDF≌△EDC,可得BF=CE,再证AD=BF即可解题.
(1)∵点D为等边三角形△ABC边AC的中点,
∴BD平分∠ABC,AD=DC
∴∠DBE=30°,
∵BD=DE,
∴∠E=∠DBE=30°,
∵∠DCE=180°-∠ACB=120°,
∴∠CDE=180°-120°-30°=30°,
∴∠CDE=∠E =30°∴DC=CE
∴AD=CE;………………4分

(2)作DF∥AB,可得△DFC是等边三角形,∴DC=CF
∴AC-DC=BC-CF ∴AD=BF
在△BDF和△EDC中,
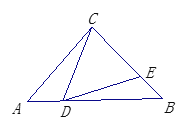
∴△BDF≌△EDC,(AAS)
∴BF=CE,
∴AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况
频数
频率
A.高度关注
M
0.1
B.一般关注
100
0.5
C.不关注
30
N
D.不知道
50
0.25
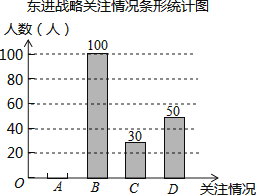
(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
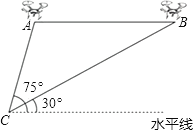
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

相关试题

