【题目】如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离. 
参考答案:
【答案】解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC, ∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE= ![]() AB=
AB= ![]() ×30=15cm,CF=
×30=15cm,CF= ![]() CD=
CD= ![]() ×16=8cm,
×16=8cm,
在Rt△AOE中,
OE= ![]() =
= ![]() =8cm,
=8cm,
在Rt△OCF中,
OF= ![]() =
= ![]() =15cm,
=15cm,
∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.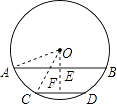
【解析】过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣1|+(﹣2)2+(7﹣π)0﹣( )﹣1
)﹣1
(2) ÷
÷ 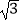 ﹣
﹣  ×
×  +
+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加家务劳动的情况,某中学随机抽取部分学生,统计他们双休日两天家务劳动的时间,将统计的劳动时间(单位:分钟)分成5组:30≤x<60,60≤x<90,90≤x<120,120≤x<150,150≤x<180,绘制成频数分布直方图.请根据图中提供的信息,解答下列问题:
(1)这次抽样调查的样本容量是;
(2)根据小组60≤x<90的组中值75,估计该组中所有数据的和为;
(3)该中学共有1000名学生,估计双休日两天有多少名学生家务劳动的时间不小于90分钟?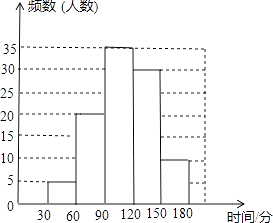
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是2个单位,一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动,另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动,则第2018次相遇在( )

A. 点A B. 点B C. 点C D. 点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】四张扑克牌的点数分别是2,3,4,8,将它们洗匀后背面朝上放在桌上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率;
(2)从中随机抽取一张牌,接着再抽取一张,求这两张牌的点数都是偶数的概率.
相关试题

