【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6 ![]() ,则FG的长为 .
,则FG的长为 . 
参考答案:
【答案】3 ![]()
【解析】解:∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD是等边三角形,
∵EG⊥AC,
∴∠AEG=∠AGE=30°,
∵∠B=∠EGF=60°,
∴∠AGF=90°,
∴FG⊥BC,
∴2S△ABC=BCFG,
∴2× ![]() ×(6
×(6 ![]() )2=6
)2=6 ![]() FG,
FG,
∴FG=3 ![]() .
.
故答案为3 ![]() .
.
首先证明△ABC,△ADC都是等边三角形,再证明FG是菱形的高,根据2S△ABC=BCFG即可解决问题.本题考查菱形的性质、等边三角形的判定和性质、翻折变换、菱形的面积等知识,记住菱形的面积=底×高=对角线乘积的一半,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件下,不能判定△ABC≌△A′B′C′是( )
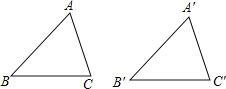
A. ∠A=∠A′,AB=A′B′,BC=B′C′ B. ∠A=∠A′,∠C=∠C′,AC=A′C′
C. ∠B=∠B′,∠C=∠C′,AC=A′C′ D. BA=B′A′,BC=B′C′,AC=A′C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是白球的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下:
油电混动汽车
普通汽车
购买价格
17.48
15.98
每百公里燃油成本(元)
31
46
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的公里数至少为( )
A. 5000 B. 10000 C. 15000 D. 20000
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AE=CF,M、N分别是BE、DF的中点,试说明四边形MFNE是平行四边形.

-
科目: 来源: 题型:
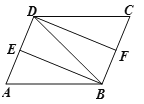
查看答案和解析>>【题目】如图,在□ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.
相关试题

