【题目】在下列条件下,不能判定△ABC≌△A′B′C′是( )
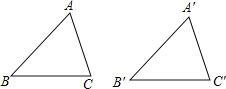
A. ∠A=∠A′,AB=A′B′,BC=B′C′ B. ∠A=∠A′,∠C=∠C′,AC=A′C′
C. ∠B=∠B′,∠C=∠C′,AC=A′C′ D. BA=B′A′,BC=B′C′,AC=A′C′
参考答案:
【答案】A
【解析】
根据“全等三角形的判定方法”结合各选项中的条件进行分析判断即可.
A选项中,条件“∠A=∠A′,AB=A′B′,BC=B′C′”满足的是“有两边和其中一边的对角对应相等”,故不能判定△ABC≌△A′B′C′;
B选项中,由条件“∠A=∠A′,∠C=∠C′,AC=A′C′”可根据“ASA”判定ABC≌△A′B′C′;
C选项中,由条件“∠B=∠B′,∠C=∠C′,AC=A′C′”可根据“AAS”判定ABC≌△A′B′C′;
D选项中,由条件“BA=B′A′,BC=B′C′,AC=A′C′”可根据“SSS”判定ABC≌△A′B′C′.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.

图1 图2
(1)求证:四边形AFCE是平行四边形;
(2)如图2,若BE⊥EC,求证:四边形ABFE是菱形.
-
科目: 来源: 题型:
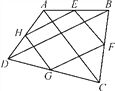
查看答案和解析>>【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是白球的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6
 ,则FG的长为 .
,则FG的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下:
油电混动汽车
普通汽车
购买价格
17.48
15.98
每百公里燃油成本(元)
31
46
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的公里数至少为( )
A. 5000 B. 10000 C. 15000 D. 20000
相关试题

