【题目】在平面直角坐标系中,O为原点,点A(0,4),点B(﹣2,0),把△ABO绕点A逆时针旋转,得△AB′O′,点B、O旋转后的对应点为B′、O′.
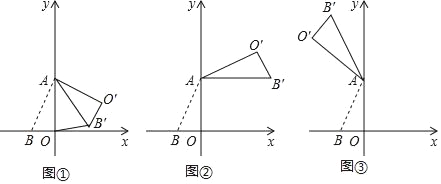
(1)如图①,若旋转角为60°时,求BB′的长;
(2)如图②,若AB′∥x轴,求点O′的坐标;
(3)如图③,若旋转角为240°时,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标(直接写出结果即可)
参考答案:
【答案】(1)![]() ;(2)点O′的坐标为(
;(2)点O′的坐标为(![]() ,
,![]() +4);(3)点P′的坐标为(﹣
+4);(3)点P′的坐标为(﹣![]() ,
,![]() .
.
【解析】分析:(1)由点A、B的坐标可得出AB的长度,连接BB′,由旋转可知:AB=AB′,∠BAB′=60°,进而可得出△ABB′为等边三角形,根据等边三角形的性质可求出BB′的长;
(2)过点O′作O′D⊥x轴,垂足为D,交AB′于点E,则△AO′E∽△ABO,根据旋转的性质结合相似三角形的性质可求出AE、O′E的长,进而可得出点O′的坐标;
(3)作点A关于x轴对称的点A′,连接A′O′交x轴于点P,此时O′P+AP′取最小值,过点O′作O′F⊥y轴,垂足为点F,过点P′作PM⊥O′F,垂足为点M,根据旋转的性质结合解直角三角形可求出点O′的坐标,由A、A′关于x轴对称可得出点A′的坐标,利用待定系数法即可求出直线A′O′的解析式,由一次函数图象上点的坐标特征可得出点P的坐标,进而可得出OP的长度,再在Rt△O′P′M中,通过解直角三角形可求出O′M、P′M的长,进而可得出此时点P′的坐标.
详解:(1)∵点A(0,4),点B(﹣2,0),∴OA=4,OB=2,∴AB=![]() =2
=2![]() .
.
在图①中,连接BB′.
由旋转可知:AB=AB′,∠BAB′=60°,∴△ABB′为等边三角形,∴BB′=AB=2![]() .
.
(2)在图②中,过点O′作O′D⊥x轴,垂足为D,交AB′于点E.
∵AB′∥x轴,O′E⊥x轴,∴∠O′EA=90°=∠AOB.
由旋转可知:∠B′AO′=∠BAO,AO′=AO=4,∴△AO′E∽△ABO,![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴AE=
,∴AE=![]() ,O′E=
,O′E=![]() ,∴O′D=
,∴O′D=![]() +4,∴点O′的坐标为(
+4,∴点O′的坐标为(![]() +4).
+4).
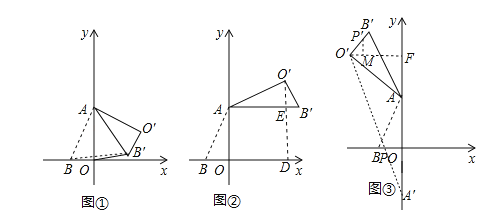
(3)作点A关于x轴对称的点A′,连接A′O′交x轴于点P,此时O′P+AP′取最小值,过点O′作O′F⊥y轴,垂足为点F,过点P′作PM⊥O′F,垂足为点M,如图3所示.
由旋转可知:AO′=AO=4,∠O′AF=240°﹣180°=60°,∴AF=![]() AO′=2,O′F=
AO′=2,O′F=![]() AO′=2
AO′=2![]() ,∴点O′(﹣2
,∴点O′(﹣2![]() ,6).
,6).
∵点A(0,4),∴点A′(0,﹣4).
设直线A′O′的解析式为y=kx+b,将A′(0,﹣4)、O′(﹣2![]() ,6)代入y=kx+b,得:
,6)代入y=kx+b,得:
![]() ,解得:
,解得: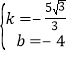 ,∴直线A′O′的解析式为y=﹣
,∴直线A′O′的解析式为y=﹣![]() x﹣4.
x﹣4.
当y=0时,有﹣![]() x﹣4=0,解得:x=﹣
x﹣4=0,解得:x=﹣![]() ,∴点P﹣
,∴点P﹣![]() ,0),∴OP=O′P′=
,0),∴OP=O′P′=![]() .
.
在Rt△O′P′M中,∠MO′P′=60°,∠O′MP′=90°,∴O′M=![]() O′P′=
O′P′=![]() ,P′M=
,P′M=![]() O′P′=
O′P′=![]() ,∴点P′的坐标为(﹣2
,∴点P′的坐标为(﹣2![]() +
+![]() ,6+
,6+![]() ),即(﹣
),即(﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AB=AC,D、E分别在AC、AB上,且BD=BC,AD=DE=EB, 则∠A的度数等于( )
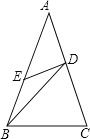
A. 36°B. 40°C. 45°D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(或方程组)解应用题2019年是决胜全面建成小康社会、打好污染防治攻坚战的关键之年.为了解决垃圾回收最后一公里的难题,“小黄狗”智能垃圾分类回收环保公益项目通过大数据、人工智能和物联网等先进科技进驻小区、写字楼、学校、机关和社区等进行回收.某位小区居民装修房屋,在过去的一个月内投放纸类垃圾和塑料垃圾共82公斤,其中纸类垃圾的投放是塑料垃圾的8倍多10公斤,请问这位小区居民在过去的一个月内投放纸类垃圾和塑料垃圾分别是多少公斤?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BE平分∠ABC,CD平分∠ACB,CD交BE 于点F,那么图中的等腰三角形共有( )个.
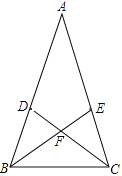
A. 6B. 7C. 8D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟)
里程数(公里)
车费(元)
小明
8
8
12
小刚
12
10
16
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别
成本价(元/箱)
销售价(元/箱)
甲
25
35
乙
35
48
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
-
科目: 来源: 题型:
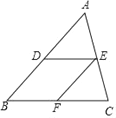
查看答案和解析>>【题目】如图,在△ABC中,D是AB中点,E是AC中点,F是BC中点,请填空:
(1)四边形BDEF是 四边形;
(2)若四边形BDEF是菱形,则△ABC满足的条件是 .
(3)若四边形BDEF是矩形,则△ABC满足的条件是 .
(4)若四边形BDEF是正方形,则△ABC满足的条件是 .
并就(2)、(3)、(4)中选取一个进行证明.
相关试题

