【题目】如图,AD为△ABC的中线,E为AD的中点,若△ABE的面积为15,则△ABC的面积为 . 
参考答案:
【答案】60
【解析】解:∵AD是△ABC的中线, S△ABD=S△ACD= ![]() S△ABC ,
S△ABC ,
∵BE是△ABD的中线,
∴S△ABE=S△DBE= ![]() S△ABD=15,
S△ABD=15,
∴S△ABD=30,
∴S△ABC=60,
所以答案是:60
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将一个自然数各位上的数字按照从高位数字到低位数字排成一列后,后一个人数减去前一个数的差是一个常数,则这个数叫做“幸福数”.如:四位数2468排成一列后为:2,4,6,8.因为8-6=6-4=4-2=2,且差为2的常数,故2468是一个差为2的四位“幸福数”.又如,9876,6666等也是“幸福数”.
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同,则称这两个数为“三生三世数”.例如:3579与9753,8765与5678,...,都是“三生三世数”.
规定:把高位数字为x,差为2的三位“幸福数”与它的“三生三世数”的和与222的商记为F(x).例如当x=5时,三位“幸福数”为579,它的“三生三世数”为975,三位“幸福数”与它的“三生三世数”的和为:579+975=1554,1554÷222=7,所以F(x)=7.
(1)计算:F(1), F(4);
(2)已知F(x) =4,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A.a2a2=2a2
B.a2+a2=a4
C.(﹣a2)2=a4
D.(a+1)2=a2+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由.
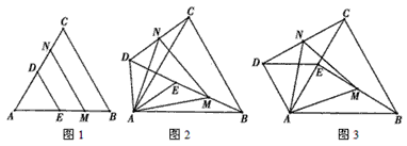
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生对体育活动的喜爱情况,某校对参加足球、篮球、乒乓球、羽毛球这四个课外活动小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供信息,解答下面问题.
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,并计算扇形统计图中的篮球部分的圆心角的度数;
(3)如果该校共有1000名学生参加这四个课外活动小组,而每个教师最多只能辅导本组20名学生,请通过计算确定每个课外活动小组至少需要准备多少名教师.
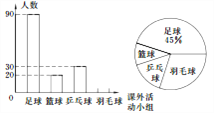
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知5x=7,5y=2,求5x+y+3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨从家里出发匀速步行去上学.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示.
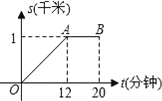
(1)试求折线段OA﹣AB所对应的函数关系式;
(2)请解释图中线段AB的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)
相关试题

