【题目】若将一个自然数各位上的数字按照从高位数字到低位数字排成一列后,后一个人数减去前一个数的差是一个常数,则这个数叫做“幸福数”.如:四位数2468排成一列后为:2,4,6,8.因为8-6=6-4=4-2=2,且差为2的常数,故2468是一个差为2的四位“幸福数”.又如,9876,6666等也是“幸福数”.
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同,则称这两个数为“三生三世数”.例如:3579与9753,8765与5678,...,都是“三生三世数”.
规定:把高位数字为x,差为2的三位“幸福数”与它的“三生三世数”的和与222的商记为F(x).例如当x=5时,三位“幸福数”为579,它的“三生三世数”为975,三位“幸福数”与它的“三生三世数”的和为:579+975=1554,1554÷222=7,所以F(x)=7.
(1)计算:F(1), F(4);
(2)已知F(x) =4,求x的值.
参考答案:
【答案】(1)F(1) =3,F(4) =6;(2) x=2.
【解析】试题分析:(1)根据题意可得“幸福数”与“三生三世数”,然后按所规定的运算顺序进行计算即可得;
(2)设三位数的最高位为x,根据定义表示出“幸福数”与“三生三世数”,然后按规定的运算顺序列出方程,解方程即可得.
试题解析:(1)由题可知,
当x=1时,“幸福数”:135;“三生三世数”:531
F(1)=(135+531)÷222=3;
同理可得,当x=4时,“幸福数”:468;“三生三世数”:864
F(4)=(468+864)÷222=6;
(2)设三位数的最高位为x,则
“幸福数”:100x+10(x+2)+(x+4);“三生三世数”:100(x+4)+10(x+2)+x
又 ![]() F(x) =4,
F(x) =4,
![]() {[100x+10(x+2)+(x+4)]+[100(x+4)+10(x+2)+x]}÷222=4,
{[100x+10(x+2)+(x+4)]+[100(x+4)+10(x+2)+x]}÷222=4,
解得,x=2.
-
科目: 来源: 题型:
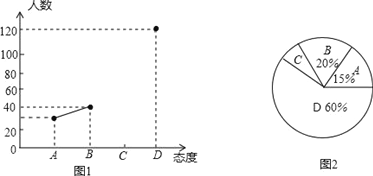
查看答案和解析>>【题目】目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
-
科目: 来源: 题型:
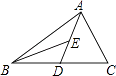
查看答案和解析>>【题目】如图,AD为△ABC的中线,E为AD的中点,若△ABE的面积为15,则△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两站相距960公里,一列慢车从A站开出,每小时行驶120公里,一列快车从B站开出,每小时行驶200公里.慢车先行1小时,快车再开,两车相向而行,慢车多少小时后两车相距200公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A.a2a2=2a2
B.a2+a2=a4
C.(﹣a2)2=a4
D.(a+1)2=a2+1 -
科目: 来源: 题型:
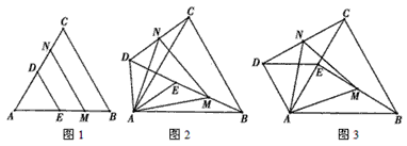
查看答案和解析>>【题目】如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,E为AD的中点,若△ABE的面积为15,则△ABC的面积为 .

相关试题

