搜索
【题目】已知，在△ABC中，∠ABC=90°，AB=4，BC=3，若线段CD=2，且CD∥AB，则AD的长度等于 ．
参考答案：
【答案】
或3 
【解析】解：分两种情况： ①如图1所示：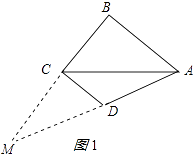
延长BC、AD交于点M，
∵CD∥AB，
∴△DCM∽△ABN，
∴ 
= 
= 
，
∴CN=BC=3，AD═ AN，
∴BN=6，
∵∠ABC=90°，
∴AN= 
= 
=2 ，
∴AD= ；
②如图2所示：
设AD交BC于O，
∵CD∥AB，∠ABC=90°，
∴△COD∽△BOA，
∴ 
= ，
∵BC=3，
∴OC=1，OB=2，
∴OD= 
= ，OA= 
=2 ，
∴AD=OA+OD=3 ；
综上所述：AD的长度等于 或3 ；
所以答案是： 或3 ．
【考点精析】关于本题考查的勾股定理的概念，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
【答案】
【解析】根据实数的运算顺序，利用二次根式性质，零指数幂法则，首先计算乘方、开方，然后从左向右依次计算．
解：原式=
．“点睛”此题主要考查了实数的运算，在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
【题型】解答题
【结束】
22【题目】已知4x2+y2 -4x-6y+10=0，求
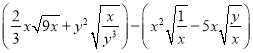的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C的度数等于（ ）
A.100°
B.105°
C.115°
D.120° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点M是边长为4cm的正方形的边AB的中点，点P是正方形边上的动点，从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动，则当点P逆时针旋转一周时，随着运动时间的增加，△DMP面积达到5cm2的时刻的个数是（ ）
A.5
B.4
C.3
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于
的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法中正确的个数是( )
①AD是∠BAC的平分线； ②∠ADC=60°；
③点D在线段ABC的垂直平分线上； ④BD=2CD.
A. 2个 B. 3个 C. 1个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，面积为48 cm2的正方形的四个角是面积为3 cm2的小正方形，请动手操作，将四个角剪掉，制作一个无盖的长方体盒子，求这个长方体盒子的底面边长.
【答案】
【解析】试题分析：根据算术平方根的定义求出大正方形和小正方形的边长，再根据底边边长的表示列式计算即可得解．
试题解析：解：正方形的边长=
=
cm，剪掉小正方形的边长=
cm，所以，长方体盒子的底面边长=
=
（cm）．答：这个长方体盒子的底面边长是
cm．点睛：本题考查了二次根式的应用，主要利用了算术平方根的定义，以及二次根式的运算．
【题型】解答题
【结束】
26【题目】已知
求(1)x2－xy＋y2；(2)x3y＋xy3的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′，则补充的这个条件是（ ）
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
相关试题
