搜索
【题目】商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场平均每天可多售出2件，每件商品降价多少元时，商场日盈利可到达2100元？
参考答案：
【答案】每件商品降价20元,商场日盈利可达2100元.
【解析】试题分析：日盈利=每件商品盈利的钱数×（原来每天销售的商品件数30+2×降价的钱数），把相关数值代入求解即可.
试题解析:设降价x元，
由题意得(50-x)(30+2x)=2100，
化简得:x2-35x+300=0，
解得:x1=15，x2=20，
该商场为了尽快减少库存,则x=15不合题意,舍去.
答:每件商品降价20元,商场日盈利可达2100元.
-
科目： 来源： 题型：
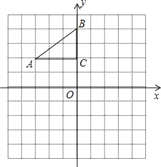
查看答案和解析>>【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；
（2）平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2 ；
（3）若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：对于任意正实数a,b，
，∴
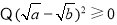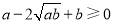，∴a+b≥2
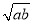，当且仅当a=b时，等号成立．结论：在a+b≥2
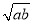（a,b均为正实数）中，若ab为定值p，则
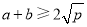，当且仅当a=b，a+b有最小值
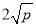．根据上述内容，回答下列问题：
（1）若x＞0，只有当x= 时，
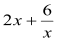有最小值 ．（2）探索应用：如图，已知A(-2,0)，B(0,-3)，点P为双曲线
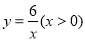上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．（3）已知x＞0，则自变量x为何值时，函数
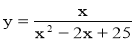取到最大值，最大值为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.
（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；
（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为： ；
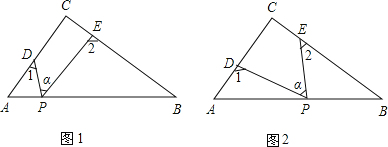
（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.
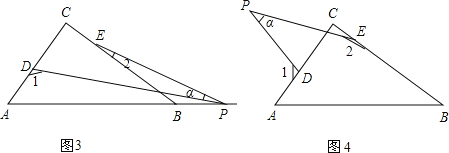
（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为： .
-
科目： 来源： 题型：
查看答案和解析>>【题目】若∣x∣=x，则x________0；若∣3+x∣=5，则x=_________
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直角三角形中一个锐角为30°，则另一个锐角为（ ）
A.30°
B.45°
C.60°
D.90° -
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A. x8÷x4=x2 B. x3x4=x12 C. （x3）2=x6 D. （﹣x2y3）2=﹣x4y6
相关试题
