【题目】阅读理解:对于任意正实数a,b,
![]() ,
,
∴![]() ,
,
∴a+b≥2![]() ,当且仅当a=b时,等号成立.
,当且仅当a=b时,等号成立.
结论:在a+b≥2![]() (a,b均为正实数)中,若ab为定值p,则
(a,b均为正实数)中,若ab为定值p,则![]() ,
,
当且仅当a=b,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
(1)若x>0,只有当x= 时,![]() 有最小值 .
有最小值 .
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线![]() 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(3)已知x>0,则自变量x为何值时,函数![]() 取到最大值,最大值为多少?
取到最大值,最大值为多少?
参考答案:
【答案】(1)32,12;(2)12,菱形;(3)5,![]() .
.
【解析】
试题分析:此题属于反比例函数综合题.考查了反比例函数的性质、菱形的判定以及阅读应用问题.注意准确理解a+b≥2![]() ,当且仅当a=b时,等号成立是关键.
,当且仅当a=b时,等号成立是关键.
(1)直接利用a+b≥2![]() ,当且仅当a=b时,等号成立;求解即可求得答案;
,当且仅当a=b时,等号成立;求解即可求得答案;
(2)首先设P(x,![]() ),则C(x,0),D(0,
),则C(x,0),D(0,![]() ),可得S四边形ABCD=
),可得S四边形ABCD=![]() ACBD=
ACBD=![]() (x+2)(
(x+2)(![]() +3),然后利用a+b≥2
+3),然后利用a+b≥2![]() ,当且仅当a=b时,等号成立求解即可求得答案;
,当且仅当a=b时,等号成立求解即可求得答案;
(3)首先设y′=![]() =x-2+
=x-2+![]() ,当x=
,当x=![]() 时y′最小,进而得出x的值以及y的值.
时y′最小,进而得出x的值以及y的值.
试题解析:(1)∵4x+9x≥2×4x×9x=12,当且仅当4x=9x时,等号成立,
∵x>0,
∴x=32,
∴若x>0,只有当x=32时,4x+9x有最小值为12;
故答案为32,12;
(2)设P(x,6x),则C(x,0),D(0,6x),
∴BD=6x+3,AC=x+2,
∴S四边形ABCD=![]() ACBD=
ACBD=![]() (x+2)(
(x+2)(![]() +3)=6+
+3)=6+![]() x+6x≥6+2
x+6x≥6+2![]() =12,
=12,
当且仅当![]() x=
x=![]() ,即x=2时,四边形ABCD面积的最小值为12,
,即x=2时,四边形ABCD面积的最小值为12,
∴OB=OD=3,OA=OC=2,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
(3)设y′=![]() =x-2+
=x-2+![]() ,
,
当x=![]() 时y′最小,
时y′最小,
∴当x=5时,y′最小=8,
∴当x=5时,y最大=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出平面直角坐标系中一个第三象限内点的坐标:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2-2x-3,当m-2≤x≤m时函数有最大值5,则m的值可能为___________
-
科目: 来源: 题型:
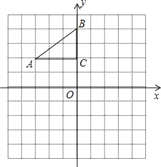
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
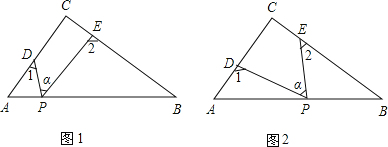
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
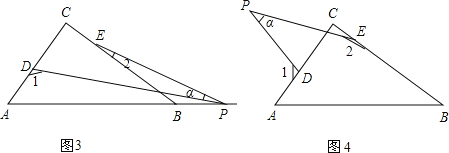
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件,每件商品降价多少元时,商场日盈利可到达2100元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∣x∣=x,则x________0;若∣3+x∣=5,则x=_________
相关试题

