【题目】兴华商店准备购进甲、乙两种书包出售,每个甲种书包的进价比每个乙种书包的进价多20元,购进3个甲种书包的费用和购进4个乙种书包的费用相等,现计划购进两种书包共100个,其中乙种书包不少于35个.
(1)甲种书包进价为__________元/个,乙种书包进价为__________元/个;
(2)若甲种书包每个售价120元,乙种书包每个售价90元,且购进这100个书包的费用不低于7200元,如果这100个书包都可售完,那么兴华商店如何进货才能获得最大利润?最大利润是多少?
参考答案:
【答案】(1)80,60;(2)最大利润为3650,此时应进65个甲书包,35个乙书包
【解析】
(1)设乙书包的进价x元/个,则甲书包的进价为(x+20)元/个,根据题意列方程即可解答;
(2)根据题意列出不等式组,求出m的取值范围,再列出w的表达式讨论即可.
(1)设乙书包的进价为x元/个,则甲书包的进价为(x+20)元/个,根据题意得:3(x+20)=4x,解得x=60,
即甲书包进价为80元/个,乙书包进价为60元/个;
(2)设计划购买m个甲书包,则购买(100-m)个乙书包,根据题意得:

解得:60≤m≤65,
设总利润为w元,
则w=(120-80)m+(90-60)(100-m)=10m+3000,
所以当m=65时,w有最大值,最大值为3650,
此时应进65个甲书包,35个乙书包.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.

(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+
 =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=
 S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平行四边形ABCD,点E在AD上,连接CE,点F为CE中点,连接DF,并且DF=EF.
(1)求证:平行四边形ABCD是矩形;
(2)如图2,过点B作BH⊥CE,垂足为H,连接AH,若∠AHB=45°,求证:AE=CD;
(3)如图3,在(2)的条件下,过点A作AK⊥BH,垂足为N,AK与BC交于点K,若四边形ABHE的面积为128,BK=2
 ,求线段HF的长度.
,求线段HF的长度.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.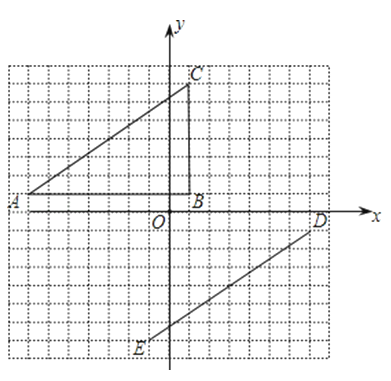
-
科目: 来源: 题型:
查看答案和解析>>【题目】 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个.某商店有两种优惠活动,如图所示.请根据以上信息,购进A种魔方多少个时,两种活动费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=2019x+2018,b=2019x+2019,c=2019x+2020.则多项式a2+b2+c2﹣ab﹣bc﹣ac的值为( )
A. 1B. 2C. 3D. 4
相关试题

