Question

【题目】某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

（1）求证：AM=AN；
（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

Answer 1

【答案】解;（1）证明：∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），
∴AB=AF，∠BAM=∠FAN，
在△ABM和△AFN中，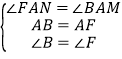
，
∴△ABM≌△AFN（ASA），
∴AM=AN；
（2）解：当旋转角α=30°时，四边形ABPF是菱形．
理由：连接AP，
∵∠α=30°，
∴∠FAN=30°，
∴∠FAB=120°，
∵∠B=60°，
∴AF∥BP，
∴∠F=∠FPC=60°，
∴∠FPC=∠B=60°，
∴AB∥FP，
∴四边形ABPF是平行四边形，
∵AB=AF，
∴平行四边形ABPF是菱形．
【解析】（1）根据旋转的性质得出AB=AF，∠BAM=∠FAN，进而得出△ABM≌△AFN得出答案即可；
（2）利用旋转的性质得出∠FAB=120°，∠FPC=∠B=60°，即可得出四边形ABPF是平行四边形，再利用菱形的判定得出答案．
【考点精析】本题主要考查了菱形的判定方法的相关知识点，需要掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能正确解答此题．