【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.
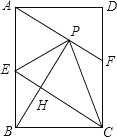
(1)若∠PBA:∠PBC=1:2,判断△PBC的形状并说明;
(2)求证:四边形AECF为平行四边形.
参考答案:
【答案】(1)△PBC是等边三角形,(2)证明见解析
【解析】
试题分析:(1)根据矩形得出∠ABC=90°,求出∠OBC=60°,根据折叠得出PC=BC,根据等边三角形的判定得出即可;
(2)根据折叠得出BE=PE,求出∠1=∠2,求出AE=PE,推出∠3=∠4,根据三角形内角和定理求出∠2+∠3=90°,求出AF∥CE,根据平行四边形的判定得出即可.
试题解析:(1)△PBC是等边三角形,
理由是:在矩形ABCD中,∠ABC=90°,
∵∠PBA:∠PBC=1:2,
∴∠OBC=60°,
∵沿EC对折矩形ABCD,使B点落在点P处,
∴PC=BC,
∴△PBC是等边三角形;
(2)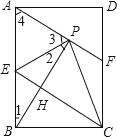
∵根据折叠得出△EBC≌△EPC,
∴BE=PE,
∴∠1=∠2,
∵E为AB的中点,
∴BE=AE,
∴AE=PE,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴BP⊥AF,
∵对折矩形ABCD,
∴BP⊥CE,
∴AF∥CE,
∵根据矩形ABCD得:AE∥CF,
∴四边形AECF为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x-2)2+3的顶点坐标是
A. (-2,3) B. (2,3) C. (2,-3) D. (-3,2)
-
科目: 来源: 题型:
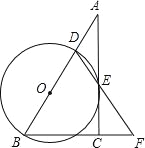
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分线,AD是高.
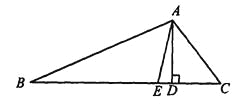
(1)求∠BAE的度数;
(2)求∠EAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值与相反数都是它的本身有( )
A. 1个 B. 2个 C. 3个 D. 不存在
-
科目: 来源: 题型:
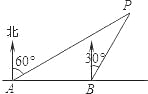
查看答案和解析>>【题目】如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
相关试题

