【题目】如图,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分线,AD是高.
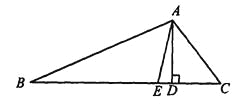
(1)求∠BAE的度数;
(2)求∠EAD的度数.
参考答案:
【答案】∠BAE为50°,∠EAD为10°。
【解析】试题分析:(1)根据△ABC的内角和定理求得∠BAC=100°;然后由角平分线的性质、△ABE的内角和定理来求∠BAE的度数;
(2)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=
![]() ∠BAC,故∠EAD=∠EAC-∠DAC.
∠BAC,故∠EAD=∠EAC-∠DAC.
解:(1)∵在△ABC中,∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°;
又∵AE是∠BAC的平分线,
∴∠BAE=![]() ∠BAC=50°;
∠BAC=50°;
(2)∵AD是边BC上的高,
∴∠ADC=90°,
∴在△ADC中,∠C=50°,∠C+∠DAC=90°,
∴∠DAC=40°,
由(1)知,∠BAE=∠CAE=50°,
∴∠DAE=∠EAC-∠DAC=50°-40°=10°,即∠EAD=10°
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x-2)2+3的顶点坐标是
A. (-2,3) B. (2,3) C. (2,-3) D. (-3,2)
-
科目: 来源: 题型:
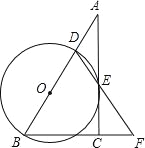
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.
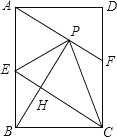
(1)若∠PBA:∠PBC=1:2,判断△PBC的形状并说明;
(2)求证:四边形AECF为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值与相反数都是它的本身有( )
A. 1个 B. 2个 C. 3个 D. 不存在
-
科目: 来源: 题型:
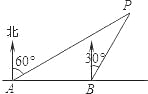
查看答案和解析>>【题目】如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=5x2的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式为( )
A. y=5(x+2)2+3 B. y=5(x﹣2)2+3
C. y=5(x+2)2﹣3 D. y=5(x﹣2)2﹣3
相关试题

