【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
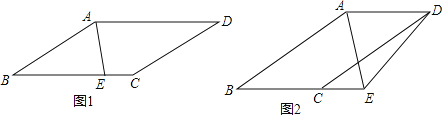
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②∠CED=135°.
【解析】
试题(1)根据平行线的性质求出∠DAE=∠BEA,由AE平分∠BAD得∠BAE=∠DAE,从而得出结论.
(2)①AD∥BC,AB∥CD即可得出结论;
②由根据∠ADE=3∠CDE设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程90-x+60+3x=180,求出x即可.
试题解析:(1)证明:∵AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA;
(2)①∵AD∥BC
∴∠ADC=∠DCE;
∵AB∥CD
∴∠ABC=∠DCE;
∴∠ABC=∠ADC;
②∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°-2x°,
由(1)可知:∠DAE=∠BAE=∠BEA=90°-x°,
∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90-x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°-∠ADE=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,
, ,
, 、
、 是
是 边上的两个动点,其中点
边上的两个动点,其中点 从点
从点 开始沿
开始沿 方向运动,且速度为每秒
方向运动,且速度为每秒 ,点
,点 从点
从点 开始沿
开始沿 方向运动,且速度为每秒
方向运动,且速度为每秒 ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为 秒.
秒.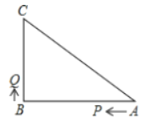
(1)当
 秒时,求
秒时,求 的长;
的长;(2)求出发时间为几秒时,
 是等腰三角形?
是等腰三角形?(3)若
 沿
沿 方向运动,则当点
方向运动,则当点 在边
在边 上运动时,求能使
上运动时,求能使 成为等腰三角形的运动时间.
成为等腰三角形的运动时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
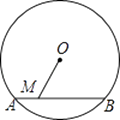
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP=
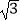 ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积;
(2)若连接AD、CF,则这两条线段之间的关系是________________ .

相关试题

