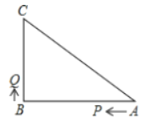
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 边上的两个动点,其中点
边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为![]() 秒.
秒.
(1)当![]() 秒时,求
秒时,求![]() 的长;
的长;
(2)求出发时间为几秒时,![]() 是等腰三角形?
是等腰三角形?
(3)若![]() 沿
沿![]() 方向运动,则当点
方向运动,则当点![]() 在边
在边![]() 上运动时,求能使
上运动时,求能使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)5.5秒或6秒或6.6秒
;(3)5.5秒或6秒或6.6秒
【解析】
(1)根据点![]() 、
、![]() 的运动速度求出
的运动速度求出![]() ,再求出
,再求出![]() 和
和![]() ,用勾股定理求得
,用勾股定理求得![]() 即可;
即可;
(2)由题意得出![]() ,即
,即![]() ,解方程即可;
,解方程即可;
(3)当点![]() 在边
在边![]() 上运动时,能使
上运动时,能使![]() 成为等腰三角形的运动时间有三种情况:
成为等腰三角形的运动时间有三种情况:
①当![]() 时(图
时(图![]() ,则
,则![]() ,可证明
,可证明![]() ,则
,则![]() ,则
,则![]() ,从而求得
,从而求得![]() ;
;
②当![]() 时(图
时(图![]() ,则
,则![]() ,易求得
,易求得![]() ;
;
③当![]() 时(图
时(图![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,则求出
,则求出![]() ,
,![]() ,即可得出
,即可得出![]() .
.
(1)解:(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)解:根据题意得:![]() ,
,
即![]() ,
,
解得:![]() ;
;
即出发时间为![]() 秒时,
秒时,![]() 是等腰三角形;
是等腰三角形;
(3)解:分三种情况:
①当![]() 时,如图1所示:
时,如图1所示:
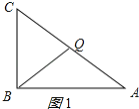
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 秒.
秒.
②当![]() 时,如图2所示:
时,如图2所示:

则![]()
![]() 秒.
秒.
③当![]() 时,如图3所示:
时,如图3所示:
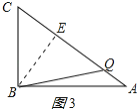
过![]() 点作
点作![]() 于点
于点![]() ,
,
则![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 秒.
秒.
由上可知,当![]() 为5.5秒或6秒或6.6秒时,
为5.5秒或6秒或6.6秒时,
![]() 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
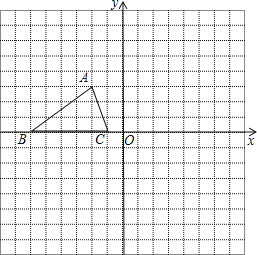
(1)请直接写出点A关于y轴对称的点的坐标为 ;
(2)将△ABC平移,使点B移动后的坐标为B′(﹣5,﹣5),画出平移后的图形△A′B′C′;
(3)将△ABC绕坐标原点O顺时针旋转90°,画出旋转后的图形△A″B″C″.
-
科目: 来源: 题型:
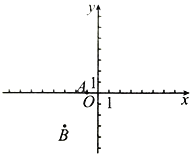
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(-1,0),B(-3,-3),若BC∥OA,且BC=4OA.
(1)求点C的坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
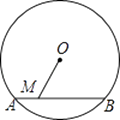
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
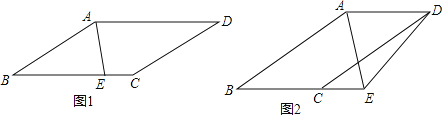
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
相关试题

