【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP= ![]() ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7
参考答案:
【答案】B
【解析】解:如图:连接OA、OD,作OE⊥AC于E,OF⊥BD于F,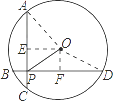
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ![]() ,
,
设OE为x(x>0),
根据勾股定理得,OF=EP= ![]() =
= ![]() ,
,
在Rt△AOE中,AE= ![]() =
= ![]()
∴AC=2AE=2 ![]() ,
,
同理得,BD=2DF=2 ![]() =2
=2 ![]() ,
,
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ![]() ,
,
∴S四边形ABCD= ![]() AC×BD=
AC×BD= ![]() ×2
×2 ![]() ×2
×2 ![]() =2
=2 ![]() =2
=2 ![]()
当x2= ![]() 即:x=
即:x= ![]() 时,四边形ABCD的面积最大,等于2
时,四边形ABCD的面积最大,等于2 ![]() =5.
=5.
答案为:B.
作出弦心距,根据S四边形ABCD=对角线乘积的一半,列出函数关系式,配成顶点式,求出最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
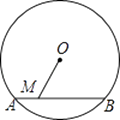
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
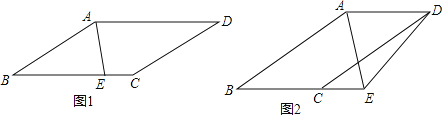
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积;
(2)若连接AD、CF,则这两条线段之间的关系是________________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一电子白板和一批笔记本电脑,经投标,购买一块电子白板比买三台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买一块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况需购买电子白板和笔记本电脑的总数为396台,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MON=51°,点P在∠MON的内部,点D是边ON上任意一点,点C是边OM上任意一点,连接PD、PC,当△PCD的周长最小时,∠CPD的度数为_______.
相关试题

