【题目】在平面直角坐标系中,直线 y1=kx+b 经过点 P(4,4)和点 Q(0,﹣4),与 x 轴交于点 A,与直线 y2=mx+n 交于点 P.
(1)求出直线 y1=kx+b 的解析式;
(2)求出点 A 的坐标;
(3)直线 y2=mx+n 绕着点 P 任意旋转,与 x 轴交于点 B,当△PAB 是等腰三角形时,直接写出点B 的坐标.

参考答案:
【答案】(1)y1=2x4;(2)A(2,0);(3)点B有4种位置使得△PAB为等腰三角形,坐标分别为(![]() +2,0)、(2
+2,0)、(2![]() ,0) 、(6,0)、(7,0).
,0) 、(6,0)、(7,0).
【解析】
(1)利用待定系数法确定函数解析式;
(2)令y=0,可求解;
(3)对于本题中的等腰△PAB的腰不确定,需要分类讨论,分三种情况:PA=AB,AB=BP,AP=BP解答.
(1)把P(4,4)和点Q(0,4)分别代入y1=kx+b,得
![]() ,
,
解得![]()
则直线y1=kx+b的解析式为:y1=2x4;
(2)∵直线y1=2x4与x轴交于点A,
∴当y=0时,0=2x4
∴x=2,
∴点A(2,0);
(3)过点P作PM⊥x轴,交于点M,
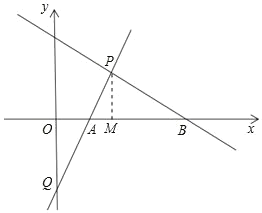
由题意可知A(2,0),M(4,0),AP=![]() ,AM=2
,AM=2
① 当AP=AB时,AB=![]() ,
,
∴B(2-![]() ,0)或者B(2+
,0)或者B(2+![]() ,0).
,0).
② 当PA=PB时,AB=2AM=4,
∴B(6,0)
③当PB=AB时,设AB=x,由勾股定理可得:42+(x-2)2=x2,
解得x=5,
∴B(7,0)
综上所述,点B有4种位置使得△PAB为等腰三角形,坐标分别为(![]() +2,0)、(2
+2,0)、(2![]() ,0) 、(6,0)、(7,0).
,0) 、(6,0)、(7,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.

(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______

(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AE⊥BD于C,AB=DE,∠A=30°,∠E=50°,F是DE的中点,则∠DBF的度数等于( )

A.10°B.20°C.30°D.40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名同学调查了全班
 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:最喜欢的节目类别
划记
人数
百分数(%)
相声
正

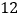
小品
正正正一


歌曲
正正


舞蹈
正一

其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈
相关试题

