【题目】已知a,b,c为正数,满足如下两个条件:
a+b+c=32 ① ![]() ② 是否存在以
② 是否存在以 ![]() ,
, ![]() ,
, ![]() 为三边长的三角形?如果存在,求出三角形的最大内角.
为三边长的三角形?如果存在,求出三角形的最大内角.
参考答案:
【答案】解:解法1:将①②两式相乘,得 ![]() ,
,
即: ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0,
即b+a=c或c+a=b或c+b=a .
因此,以 ![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.
解法2:结合①式,由②式可得 ![]() ,
,
变形,得 ![]() ③
③
又由①式得(a+b+c)2=1024,即a2+b2+c2=1024﹣2(ab+bc+ca),
代入③式,得 ![]() ,
,
即abc=16(ab+bc+ca)﹣4096.(a﹣16)(b﹣16)(c﹣16)=abc﹣16(ab+bc+ca)+256(a+b+c)﹣163=﹣4096+256×32﹣163=0,
所以a=16或b=16或c=16.
结合①式可得b+a=c或c+a=b或c+b=a .
因此,以 ![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.
【解析】解法一:根据已知,将两式相乘,运用平方差公式、完全平方式、提取公因式将乘积分解为 ![]() .再根据每个因式都可能等于零,及勾股定理,判断三角形为直角三角形.最大角度也就是90°
.再根据每个因式都可能等于零,及勾股定理,判断三角形为直角三角形.最大角度也就是90°
解法二:将①式变形代入,求出a、b、c的值,再利用勾股定理,判断三角形的为直角三角形.最大角度也就是90°.本题考查因式分解的应用.解决本题的关键是运用因式分解、等式变形求出a、b、c三角形三边的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣3x=0的解是( )
A.x=3B.x=0C.x=1或x=3D.x=3 或x=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】为测山高,在点A处测得山顶D的仰角为31°,从点A向山方向前进140米到达点B,在B处测得山顶D的仰角为62°(如图).

(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C;
(2)山高DC是多少(结果取整数)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a、b、c为何值时,代数式
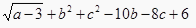 有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积.
有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数
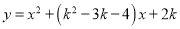 的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.(1)求k的值;
(2)在(1)的条件下,若反比例函数
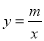 的图象与二次函数
的图象与二次函数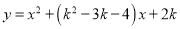 的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(
的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(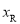 ,
, 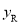 ),S(
),S(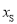 ,
, 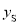 )中的纵坐标
)中的纵坐标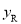 ,
, 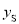 分别是一元二次方程
分别是一元二次方程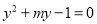 的解,求四边形AQBS的面积
的解,求四边形AQBS的面积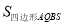 ;
;(3)在(1),(2)的条件下,在x轴下方是否存在二次函数
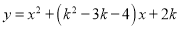 图象上的点P使得
图象上的点P使得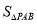 =2
=2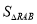 ,若存在,求出点P的坐标;若不存在,请说明理由.
,若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:
503×497=_______;1.02×0.98=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,问:甲巡逻艇的航向是多少?

相关试题

