【题目】如图,已知点O在线段AB上,点C,D分别是AO,BO的中点![]()
(1)AO=CO;BO=DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
参考答案:
【答案】
(1)2,2
(2)解:根据(1)的结论可得:AO=6cm;BO=4cm,
则AB=AO+BO=6+4=10cm
(3)解:任然成立.
理由如下:如图所示:

根据题意得:CO= ![]() AO,DO=
AO,DO= ![]() BO
BO
∴CD=CO-DO
= ![]() AO-
AO- ![]() BO
BO
= ![]() (AO-BO)
(AO-BO)
= ![]() AB=
AB= ![]() ×10=5cm.
×10=5cm.
【解析】(1)根据题意可得:AO=2CO;BO=2DO
(1)根据线段中点的定义,可求解。
(2)根据线段中点的定义先求出AO、BO的长,再根据AB=AO+BO,即可求得AB的长。
(3)根据线段中点的定义先求出CO、DO的长,再根据CD=CO-DO,代入求值即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度
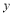 (微克/毫升)与服药时间
(微克/毫升)与服药时间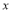 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当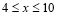 时,
时,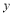 与
与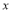 成反比).
成反比).
(1)根据图象分别求出血液中药物浓度上升和下降阶段
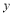 与
与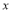 之间的函数关系式;
之间的函数关系式;(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
A.长度相等的弧是等弧B.相等的圆心角所对的弦相等
C.等边三角形的外心与内心重合D.任意三点可以确定一个圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=
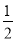 GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH其中,正确的结论有( )
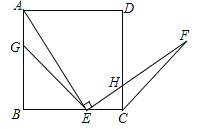
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE与E点.
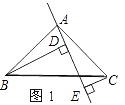
(1)求证:BD=DE+CE
(2)若直线AE绕点A旋转到图2所示的位置时(BD<CE)其余条件不变,问BD 与DE,CE的关系如何?请予以证明.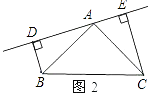
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE)其余条件不变,问BD 与DE,CE的关系如何?直接写出结果,不需证明.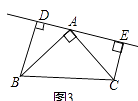
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF,下列结论错误的是( )
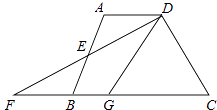
A.△ADE≌△BFE
B.AD+BG=DG
C.连接EG,EG∥DC
D.连接EG,EG⊥DF
相关试题

