【题目】某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
等级 | 成绩x/分 | 频数/(人数) | 频率 |
A | 9.0≤x≤10.0 | a | m |
B | 7.0≤x<9.0 | 23 | 0.46 |
C | 6.0≤x<7.0 | b | n |
D | 0.0≤x<6.0 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)在被调查的男生中,成绩为B等级的有多少人,占被调查男生人数的多少,m 等于 多少;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.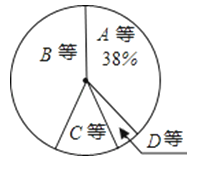
参考答案:
【答案】解:(1)根据频数分布表知,B等级人数为23人,占被调查人数的46%,由扇形统计图可知A等级的频率为38%=0.38;
(2)a=50×0.38=19,
b=50﹣(19+23+3)=5,
n=5÷50=0.1;
(3)(0.38+0.46)×200=168(人)
故这200名男生中成绩达到A等级和B等级的大约有168人.
故答案为:(1)23,46,0.38.
【解析】(1)根据频数分布表知B等级的人数、占被调查男生人数的百分比,由扇形统计图可知A等级的频率;
(2)根据A等级频数=总人数×A等级频率可得a的值,用总人数减去其余三组人数和可得b的值,用C等级人数÷总人数可得n的值;
(3)用七年级总人数乘以A、B等级的频率和可估计人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为 .
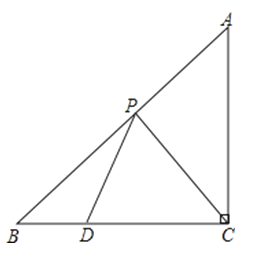
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处时,四边形AECF是矩形?并说出你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.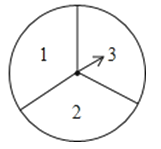
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.
(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?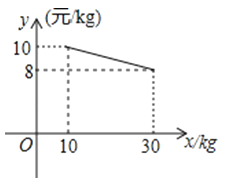
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
相关试题

