搜索
【题目】如图，已知直线
的解析式是
，并且与
轴、
轴分别交于A、B两点．一个半径为1.5的⊙C，圆心C从点（0，1.5）开始以每秒0.5个单位的速度沿着
轴向下运动，当⊙C与直线
相切时，则该圆运动的时间为（ ）
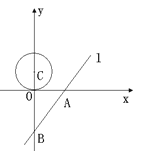
A. 3秒或6秒 B. 6秒 C. 3秒 D. 6秒或16秒
参考答案：
【答案】D
【解析】试题解析：如图，
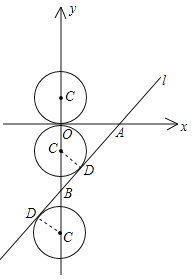
∵x=0时，y=-4，
y=0时，x=3，
∴A（3，0）、B（0，-4），
∴AB=5，
当C在B上方，直线与圆相切时，连接CD，
则C到AB的距离等于1.5，
∴CB=1.5÷sin∠ABC=1.5×
=2.5；
∴C运动的距离为：1.5+（4-2.5）=3，运动的时间为：3÷0.5=6；
同理当C在B下方，直线与圆相切时，
连接CD，则C运动的距离为：1.5+（4+2.5）=8，运动的时间为：8÷0.5=16．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=
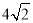，则△CEF的周长为（ ）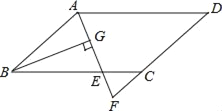
A. 8 B. 9.5 C. 10 D. 11.5
-
科目： 来源： 题型：
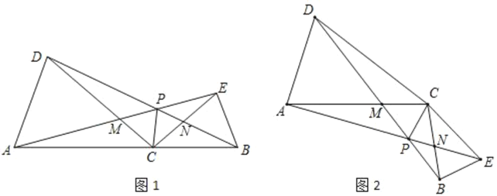
查看答案和解析>>【题目】如图1，点C为线段AB上任意一点（不与点A、B重合），分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE，CA＝CD，CB＝CE，∠ACD＝∠BCE＝30°，连接AE交CD于点M，连接BD交CE于点N，AE与BD交于点P，连接CP．
（1）线段AE与DB的数量关系为 ；请直接写出∠APD＝ ；
（2）将△BCE绕点C旋转到如图2所示的位置，其他条件不变，探究线段AE与DB的数量关系，并说明理由；求出此时∠APD的度数；
（3）在（2）的条件下求证：∠APC＝∠BPC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D是BC边的中点，点E，F分别在AC，AB上，且DE∥AB，EF∥BC．
（1）求证：CD＝EF；
（2）已知∠ABC＝60°，连接BE，若BE平分∠ABC，CD＝6，求四边形BDEF的周长．
-
科目： 来源： 题型：
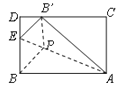
查看答案和解析>>【题目】矩形纸片ABCD中，AB＝3，AD＝4，将纸片折叠，使点B落在边CD上的B’处，折痕为AE．在折痕AE上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为_______．
-
科目： 来源： 题型：
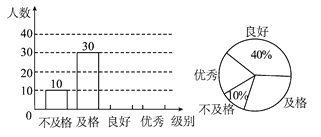
查看答案和解析>>【题目】5月19日，中国首个旅游日正式启动，某校组织了由八年级800名学生参加的旅游地理知识竞赛．李老师为了了解对旅游地理知识的掌握情况，从中随机抽取了部分同学的成绩作为样本，把成绩按优秀、良好、及格、不及格4个级别进行统计，并绘制成了如图所示的条形统计图和扇形统计图（部分信息未给出）．
请根据以上提供的信息，解答下列问题：
（1）求被抽取的部分学生的人数；
（2）请补全条形统计图，并求出扇形统计图中表示及格的扇形的圆心角度数；
（3）请估计八年级的800名学生中达到良好和优秀的总人数．
-
科目： 来源： 题型：
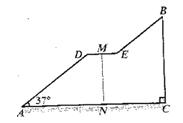
查看答案和解析>>【题目】如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成．已知天桥高度BC≈4.8米，引桥水平跨度AC=8米．
（1）求水平平台DE的长度；
（2）若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比．
（参考：sin37°=0.60，cos37°=0.80，tan37°=0.75）
相关试题
