【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒. 
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB第一次能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
参考答案:
【答案】
(1)解:BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm,
∵∠B=90°,
PQ= ![]() =
= ![]() =
= ![]() =2
=2 ![]()
(2)解:BQ=2t,
BP=8﹣t
2t=8﹣t,
解得:t= ![]()
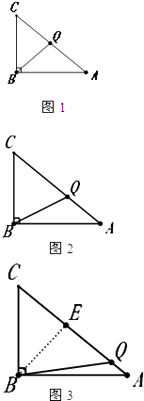
(3)解:①当CQ=BQ时(图1),则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时(如图2),则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,
则BE= ![]() =
= ![]() ,
,
所以CE= ![]() ,
,
故CQ=2CE=7.2,
所以BC+CQ=13.2,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
【解析】(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=8﹣t,列式求得t即可;(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;②当CQ=BC时(如图2),则BC+CQ=12,易求得t;③当BC=BQ时(如图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
 (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20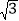 ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.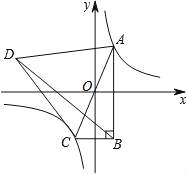
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2x﹣3)(x+1)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A. 明年国庆节宁波的天气是晴天B. 小华上学的路上遇到同班同学
C. 任意掷一枚均匀的硬币,正面朝上D. 在学校操场上抛出的篮球会下落
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两相似三角形对应高的比为3:10,且这两个三角形的周长差为56cm,则较小的三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( ) (1.)△ABC是等腰三角形 (2.)BF=AC
(3.)BH:BD:BC=1: (4.)GE2+CE2=BG2 .
(4.)GE2+CE2=BG2 . 
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小彬骑自行车去郊外游玩,事先决定早晨8点出发,预计每小时骑7.5千米,上午10时可到达目的地.出发前他们决定上午9点到达目的地,那么实际每小时要骑千米.
相关试题

